前言
本文的是台湾大学2020机器学习的Classification1和2的笔记,奉行Lazy evaluation策略,对这些知识更深层次的探究只在绝对必要时完成。
分类
在分类问题,我们要找一个函数f,f的输入是代表样本的向量,输出是一个代表类别的标量。将样本分为两类的叫做二元分类,多于两类的叫做多元分类。我们先考虑二元分类问题。
引例
XCOM中面对的敌人有变种人(ADVENT)和外星人(Alien)两种,长老(The elder)送来了新的物种,现有训练资料变种人数据15组,外星人10组,你能据此帮助被关在外星人网络中充当首脑的人类指挥官分辨新物种的种类吗?
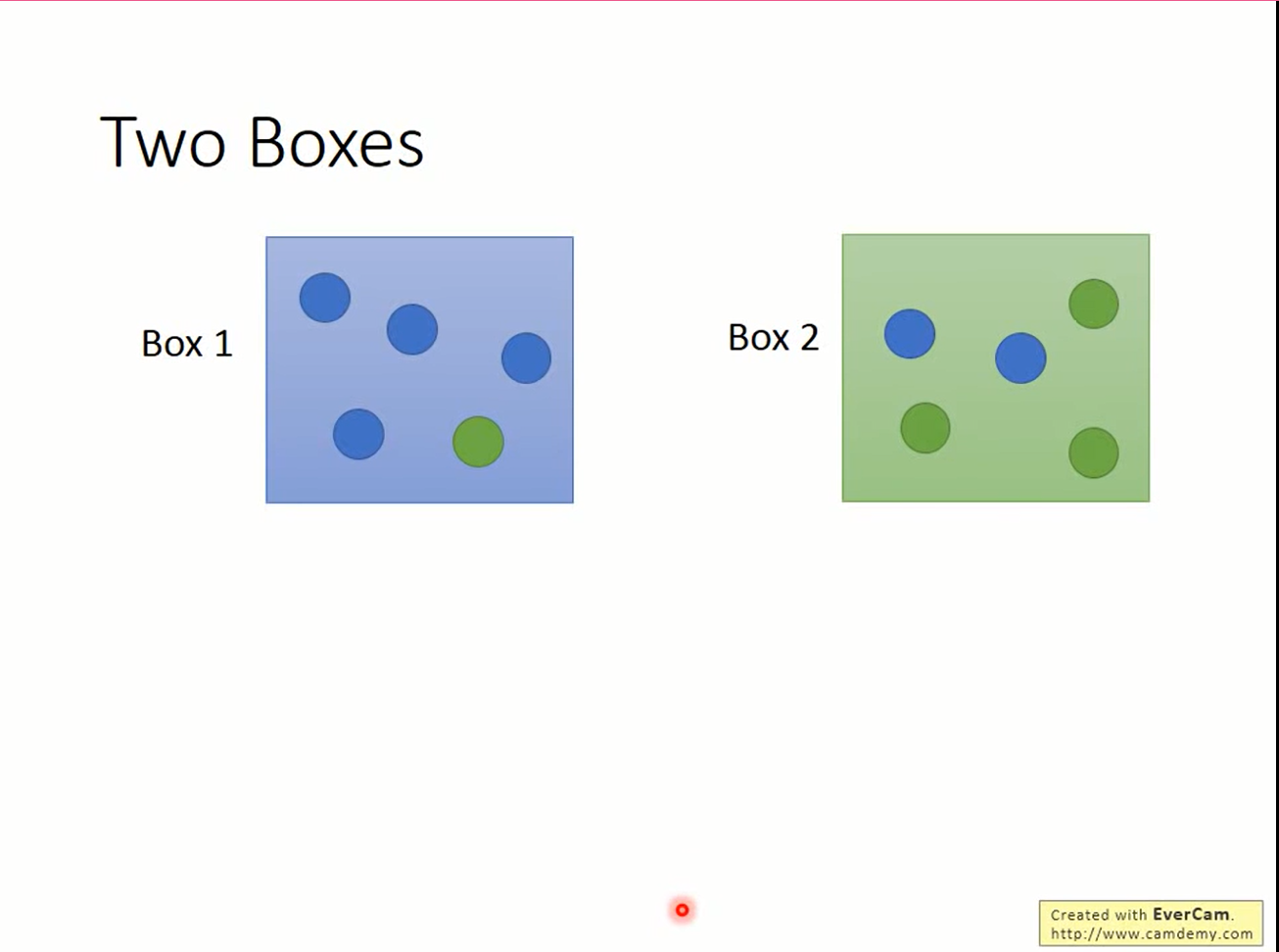
先考虑这个问题,蓝绿两个盒子,其中各有蓝绿球若干。从蓝盒子抽球的概率是1/3,从绿盒子抽球的概率是2/3。已知抽到了蓝球,问从蓝色盒子里抽到的概率是多少?
贝叶斯公式
我们预测的依据是贝叶斯公式:
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$用C1表示敌人属于变种人,C2表示敌人属于外星人,那么
$$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P({x|C_2})P(C_2))}$$training set中一共有15组变种人,10组外星人。则
$$ P(C_1)=\frac{15}{15+10}=\frac{3}{5} \\ P(C_2)=\frac{10}{15+10}=\frac{2}{5} $$接下来是确定P(x|C1)。思考一下,testing-set上的数据我们的算法从来没有见过,那么P(x|C1)应该是0咯。可这样贝叶斯公式就变成0/0了,还怎么预测?
P(C1|x)
在此,我们大胆假设,目前所见过的C1的example是由一个概率分布产生的,这样就可以对testing-set上没见过的数据了求概率了。
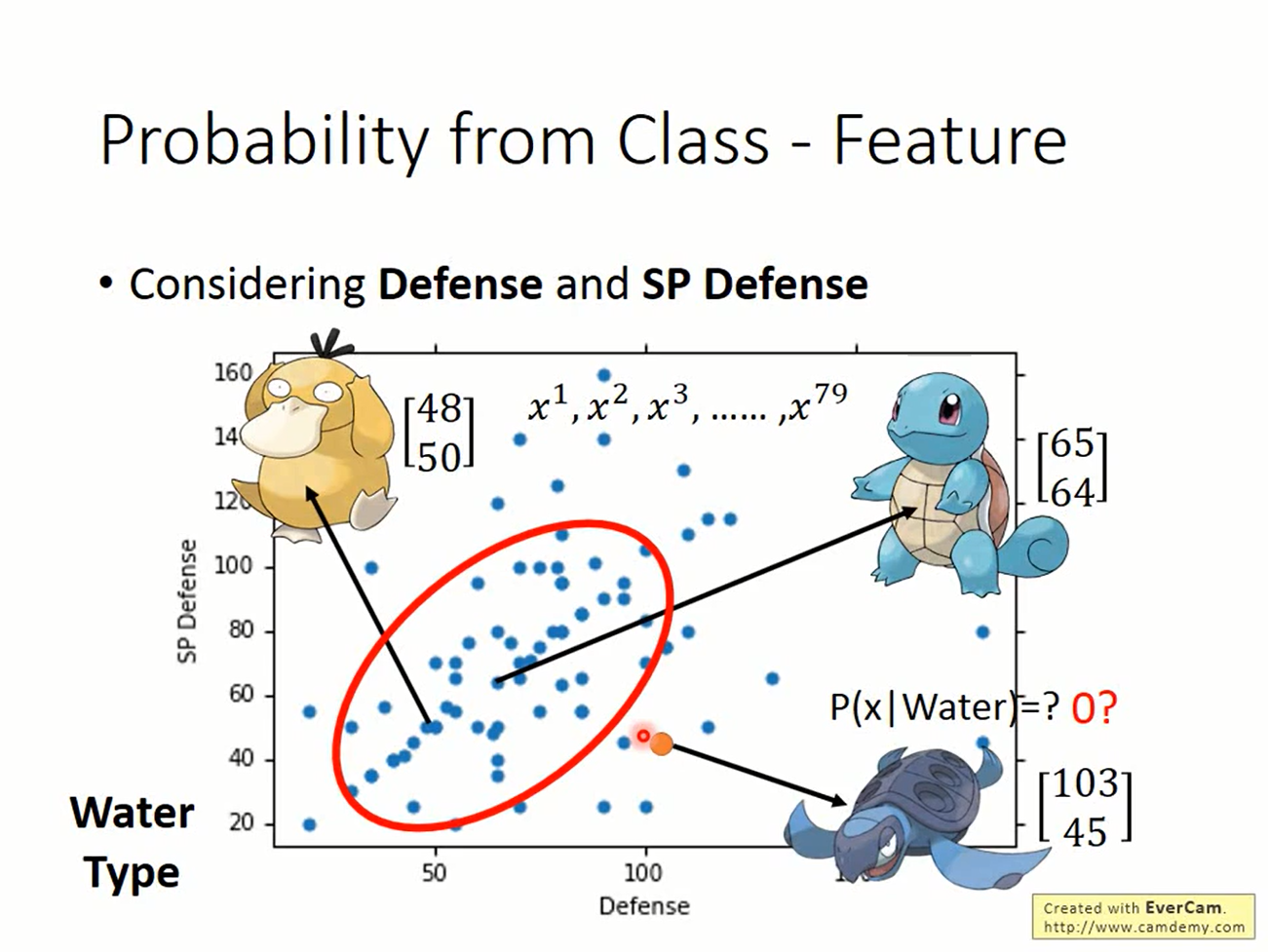
这是课件的一张图,对于图中79个example,认为是一个Gaussian产生的,但好多个Gaussian都可以产生这样的点,具体是哪一个呢?这里使用极大似然的思想,就认为使得产生训练数据的概率最大的Gaussian好了
回到我们的例子,似然函数是
$$ L(\mu,\Sigma)=\prod_i^{15}f_{\mu,\Sigma}(x^i) \\ f_{\mu,\Sigma}=\frac{1}{2\pi^{D/2}}\frac{1}{|\Sigma|^{1/2}}\exp{\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\}} \\ \mu^*,\Sigma^*=\argmax_{\mu,\Sigma} L(\mu,\Sigma) $$经过一番运算后,得到μ和Σ的闭式解:
$$ \mu^*=\frac{1}{15}\sum_{n=1}^{15}x^n \Sigma^*=\frac{1}{15}\sum_{n=1}^{15}(x^n-\mu^*)(x^n-\mu^*)^T $$
这样就得到了C1的分布G1(μ,Σ),同理可以得到C2的分布G2(μ,Σ),有了这两项就可以计算条件概率从而完成预测了。
|
|
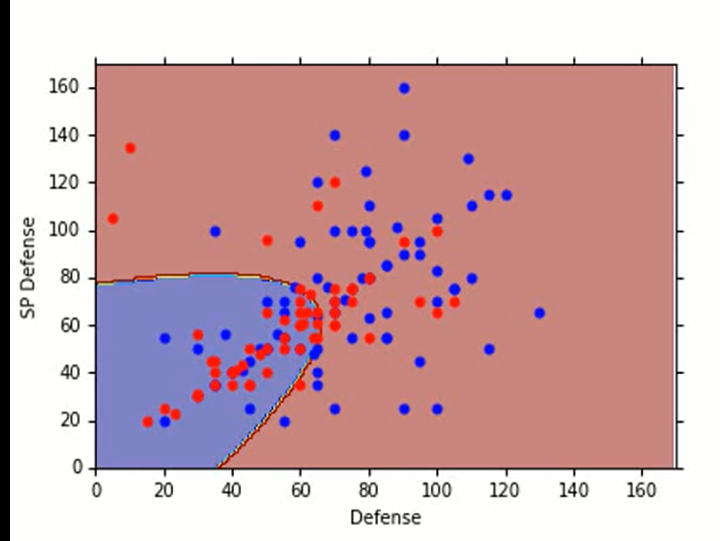 回到上课的例子,这个模型的效果并不好:(。
回到上课的例子,这个模型的效果并不好:(。
想到Probability中Gaussion的PS
如果用高斯分布来做分类问题,让分布共用协方差矩阵Σ通常效果会比使用各自的协方差矩阵效果好。
那就试试共用协方差矩阵吧
共用协方差矩阵
似然函数变为
$$ L(\mu_1,\mu_2,\Sigma)=\prod_i^{15}f_{\mu1,\Sigma}(x^i)\prod_{j=16}^{25}f_{\mu2,\Sigma}(x^i) \\ $$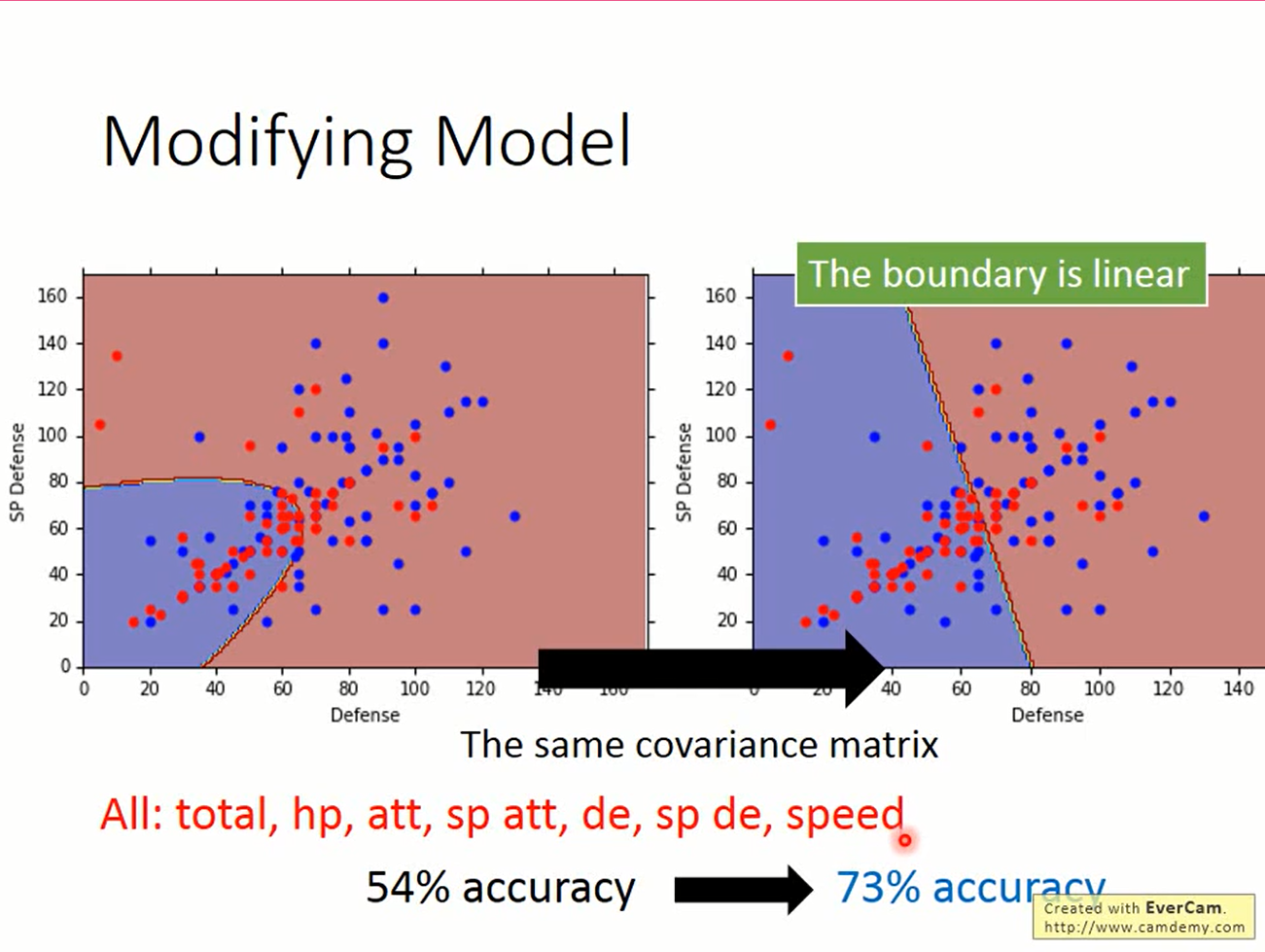 求解过程省略,来看一下结果,准确度一下子就上来了。这时发现分界线变成了一条直线。这与线性模型有关系吗?推一下看看
求解过程省略,来看一下结果,准确度一下子就上来了。这时发现分界线变成了一条直线。这与线性模型有关系吗?推一下看看
Why linear?一些推导
$$ P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P({x|C_2})P(C_2))} \\ $$上下同除以分子
$$ P(C_1|x)=\frac{1}{1+\frac{P({x|C_2})P(C_2)}{P(x|C_1)P(C_1)}} $$$$ 令z=\ln \frac{P({x|C_1})P(C_1)}{P(x|C_2)P(C_2)}, 则P(C_1|x)=\frac{1}{1+\exp(-z)}=\sigma(z) $$sigmoid函数就这样出现了! 继续分解z
$$ z=\ln \frac{P({x|C_1})P(C_1)}{P(x|C_2)P(C_2)}=\ln \frac{P({x|C_1})}{P(x|C_2)}+\ln\frac{P(C_1)}{P(C_2)} $$$$
\lg \frac{P(C_1)}{P(C_2)}=\lg \frac{\frac{N_1}{N_1+N_2}}{\frac{N_2}{N_1+N_2}}=\lg \frac{N_1}{N2}
$$ 是个常数 $$P(x|C_1)=\frac{1}{2\pi^{D/2}}\frac{1}{|\Sigma|^{1/2}}\exp{{-\frac{1}{2}(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)}}
$$ $$P(x|C_2)=\frac{1}{2\pi^{D/2}}\frac{1}{|\Sigma|^{1/2}}\exp{{-\frac{1}{2}(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)}}
$$ 带入,则 $$\ln \frac{P({x|C_1})}{P(x|C_2)} = \ln \frac{\frac{1}{2\pi^{D/2}}\frac{1}{|\Sigma|^{1/2}}\exp{{-\frac{1}{2}(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)}}}{\frac{1}{2\pi^{D/2}}\frac{1}{|\Sigma|^{1/2}}\exp{{-\frac{1}{2}(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)}}}
$$ $$=\ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} +\ln \exp\lgroup -\frac{1}{2}[(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)-(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)]\rgroup
$$ $$= \ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} +\lgroup -\frac{1}{2}[(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)-(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)]\rgroup
$$ $$= \ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} +\lgroup -\frac{1}{2}[x^T(\Sigma^1)^{-1}x-2(\mu^1)^T(\Sigma^1)^{-1}x+(\mu^1)^T(\Sigma^1)^{-1}\mu^1-x^T(\Sigma^2)^{-1}x+2(\mu^1)^T(\Sigma^2)^{-1}x-(\mu^2)^T(\Sigma^2)^{-1}\mu^2]\rgroup
$$ $$z= \ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} +\lgroup -\frac{1}{2}[x^T(\Sigma^1)^{-1}x-2(\mu^1)^T(\Sigma^1)^{-1}x+(\mu^1)^T(\Sigma^1)^{-1}\mu^1-x^T(\Sigma^2)^{-1}x+2(\mu^1)^T(\Sigma^2)^{-1}x-(\mu^2)^T(\Sigma^2)^{-1}\mu^2]\rgroup + \lg \frac{N_1}{N2} $$
共用协方差矩阵时,
$$\Sigma^1=\Sigma^2=\Sigma $$$$ \ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} =0 x^T(\Sigma^1)^{-1}x - x^T(\Sigma^2)^{-1}x=0 $$此时
$$z = (\mu^1-\mu^2)^T\Sigma^{-1}x-\frac{1}{2}(\mu^1)^T(\Sigma)^{-1}\mu^1+\frac{1}{2}(\mu^2)^T\Sigma^{-1}\mu^2+\ln \frac{N_1}{N2} $$$$ 令w^T=(\mu^1-\mu^2)^T\Sigma^{-1},b=-\frac{1}{2}(\mu^1)^T(\Sigma)^{-1}\mu^1+\frac{1}{2}(\mu^2)^T\Sigma^{-1}\mu^2+\ln \frac{N_1}{N2}$$$$则z=w^T+b $$$$P(C_1|x)= \sigma(z)$$是z的广义线性模型,给它一个名字,即logistic regression。
由
$$\mu^2,\mu^2,\Sigma^1,\Sigma^2$$得到w和b的模型称为生成模型(generative model),因为各个x可以由一组分布生成出来。 直接找出w和b的模型称为判别模型(discriminative model)
logistic regression
Step1, find a function set
logistic regression问题中,我们要找一组参数w和b,σ(wTx+b)给出的值是x属于正例的概率。
Step2, determine goodness of function
这里使用似然函数

最小化对数似然函数(NLL)实际上就是最小化交叉熵

Step3, find the best function
梯度下降走你
Why likelihood instead of MSE?

若使用MSE,则偏微分的值一直是0,无法进行梯度下降。
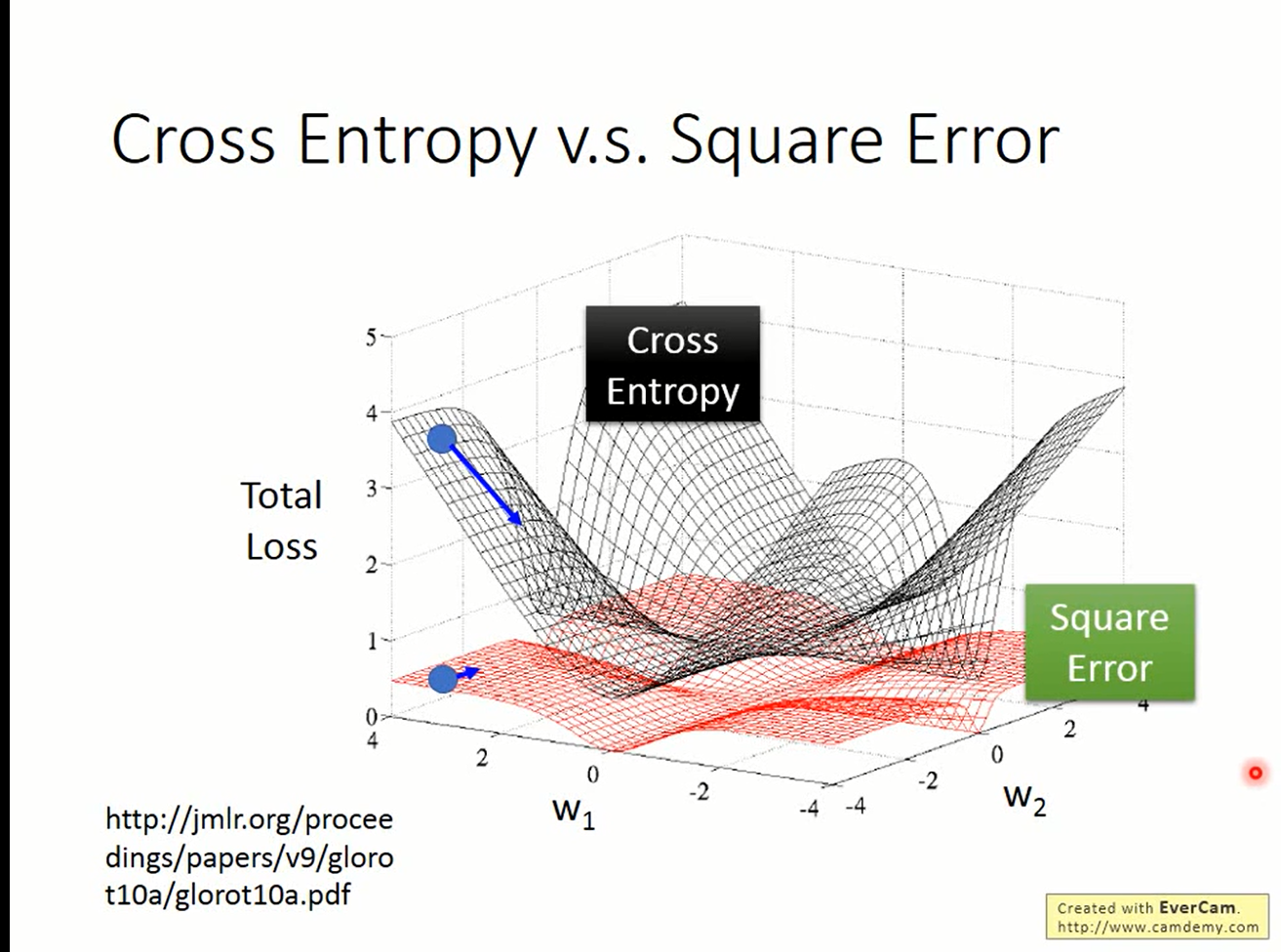 由图可见,在logistic regression这个问题上,交叉熵(极大似然)确实比MSE的梯度更大,更适合当作评价函数好坏的标准。
由图可见,在logistic regression这个问题上,交叉熵(极大似然)确实比MSE的梯度更大,更适合当作评价函数好坏的标准。
多元分类
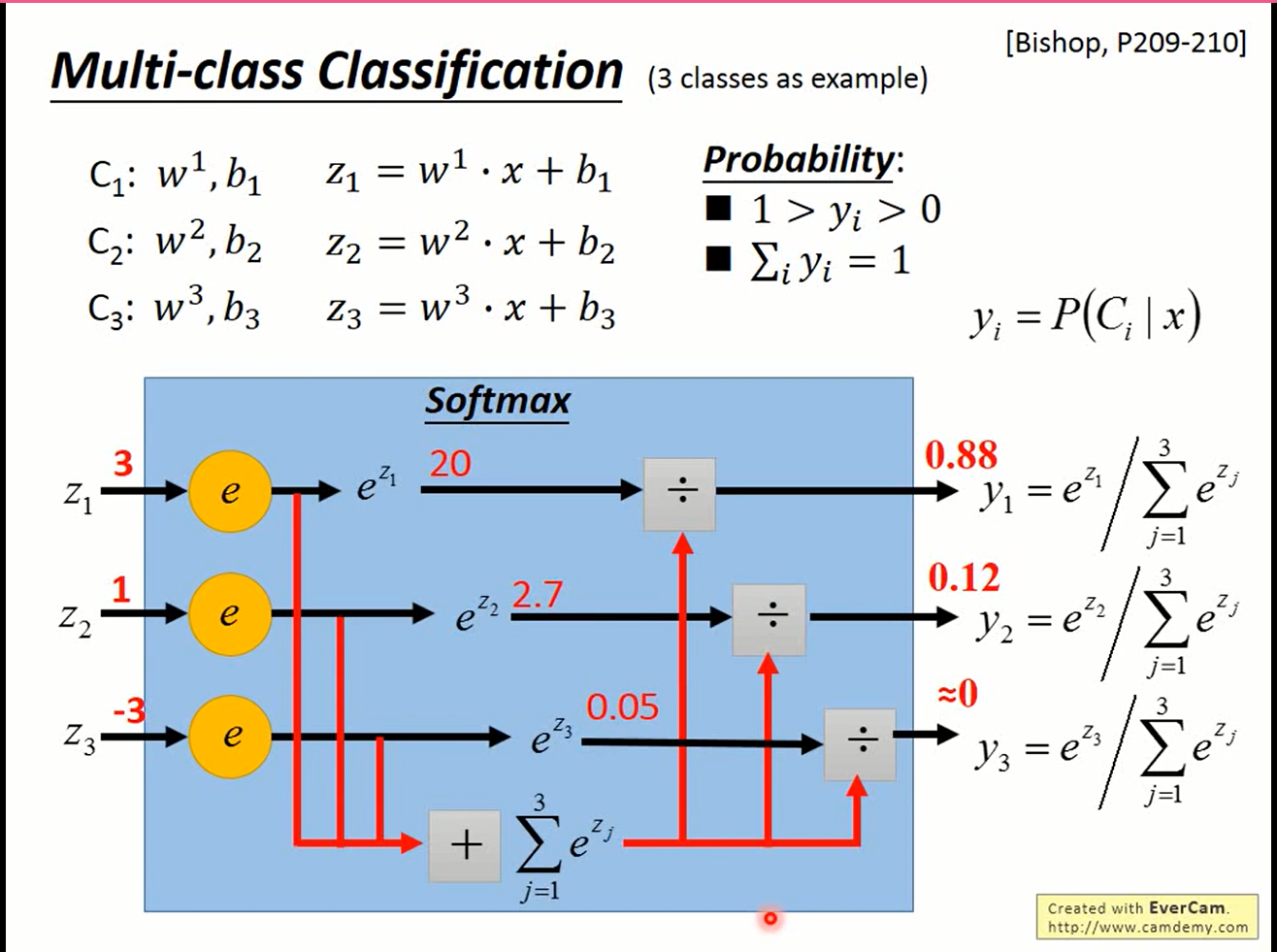
Step 1
以三元分类为例,要做三元分类,要找三组参数
$$ C_1:w^1,b^1 \text{ } z_1=w^1x+b_1 \ C_2:w^2,b^2 \text{ } z_2=w^2x+b_2 \ C_3:w^3,b^3 \text{ } z_3=w^3x+b_3 \ \mathrm{softmax}: \vec{z} \in \mathbb{R}^n\to \vec{y} \in\mathbb{R}^n \ \text{}\\ y_i = \frac{\exp{z_i}}{\sum_{i=1}^3}
$$
Step 2
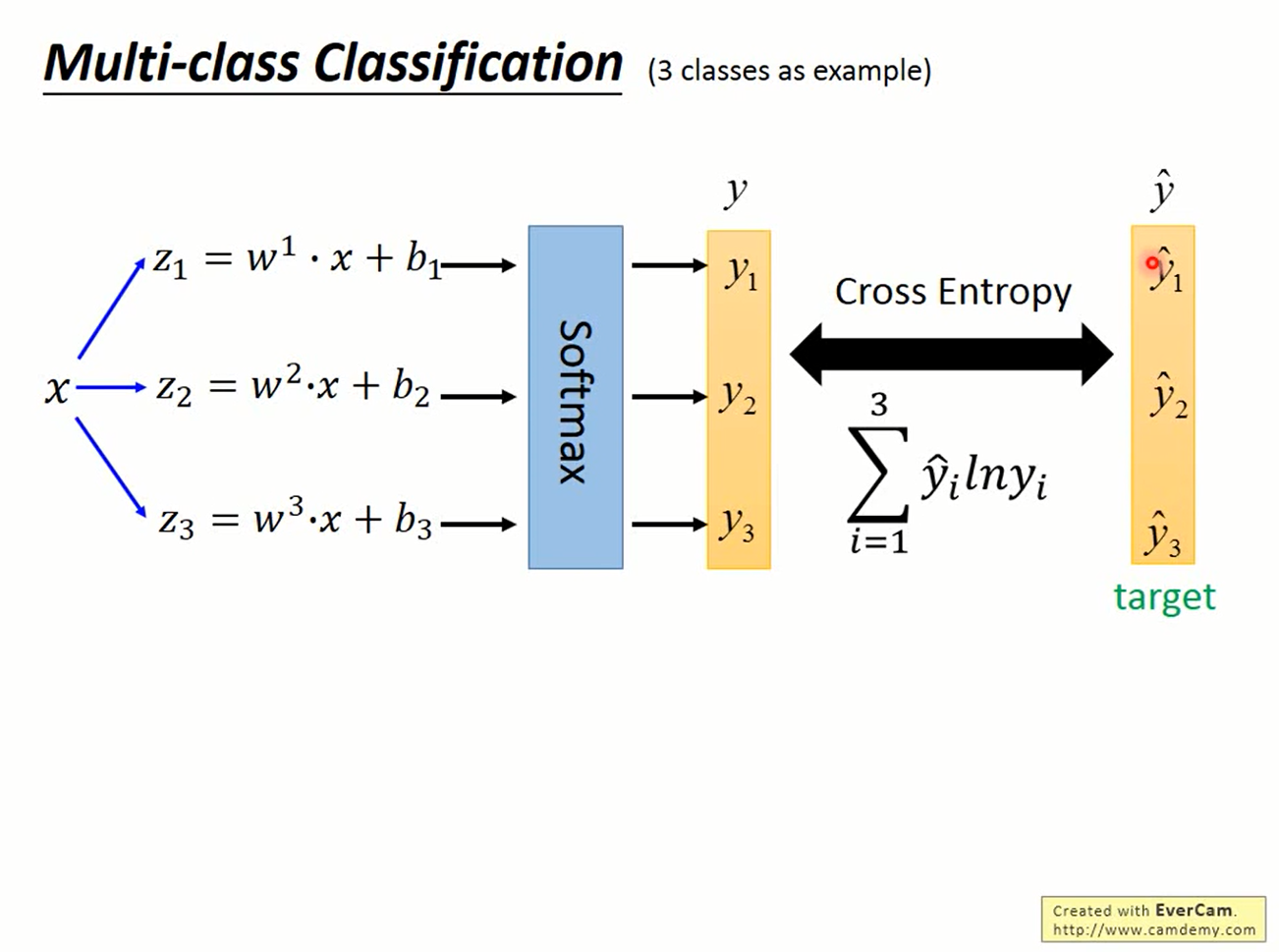
把z经过softmax函数变换后得到的概率分布y与真实值计算交叉熵,即为需要最小化的函数
Step 3
梯度下降
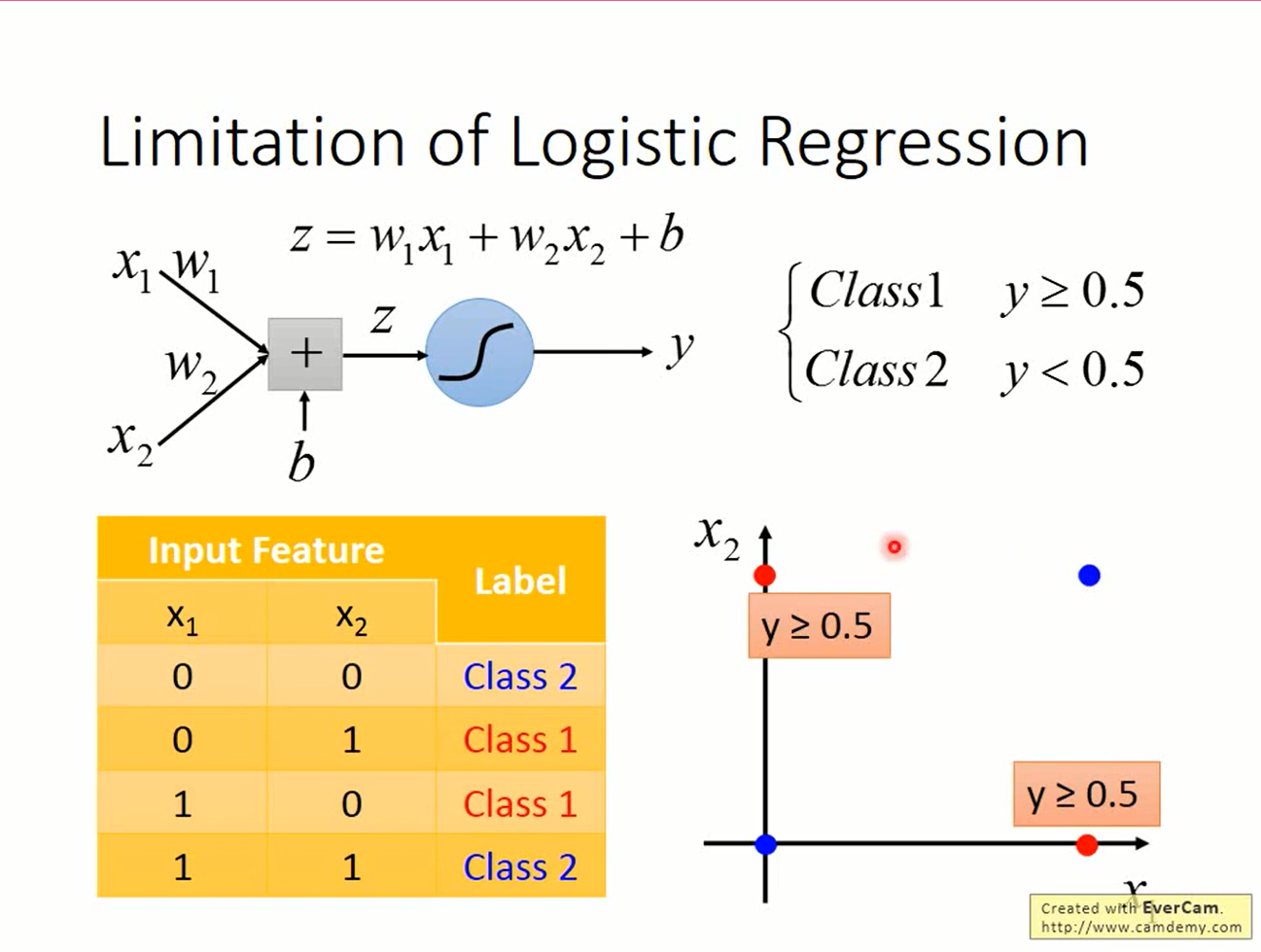
线性模型的限制
线性模型的函数是直线,而稍微复杂点的问题是无法用直线解决的。例如XOR问题
feature transformation
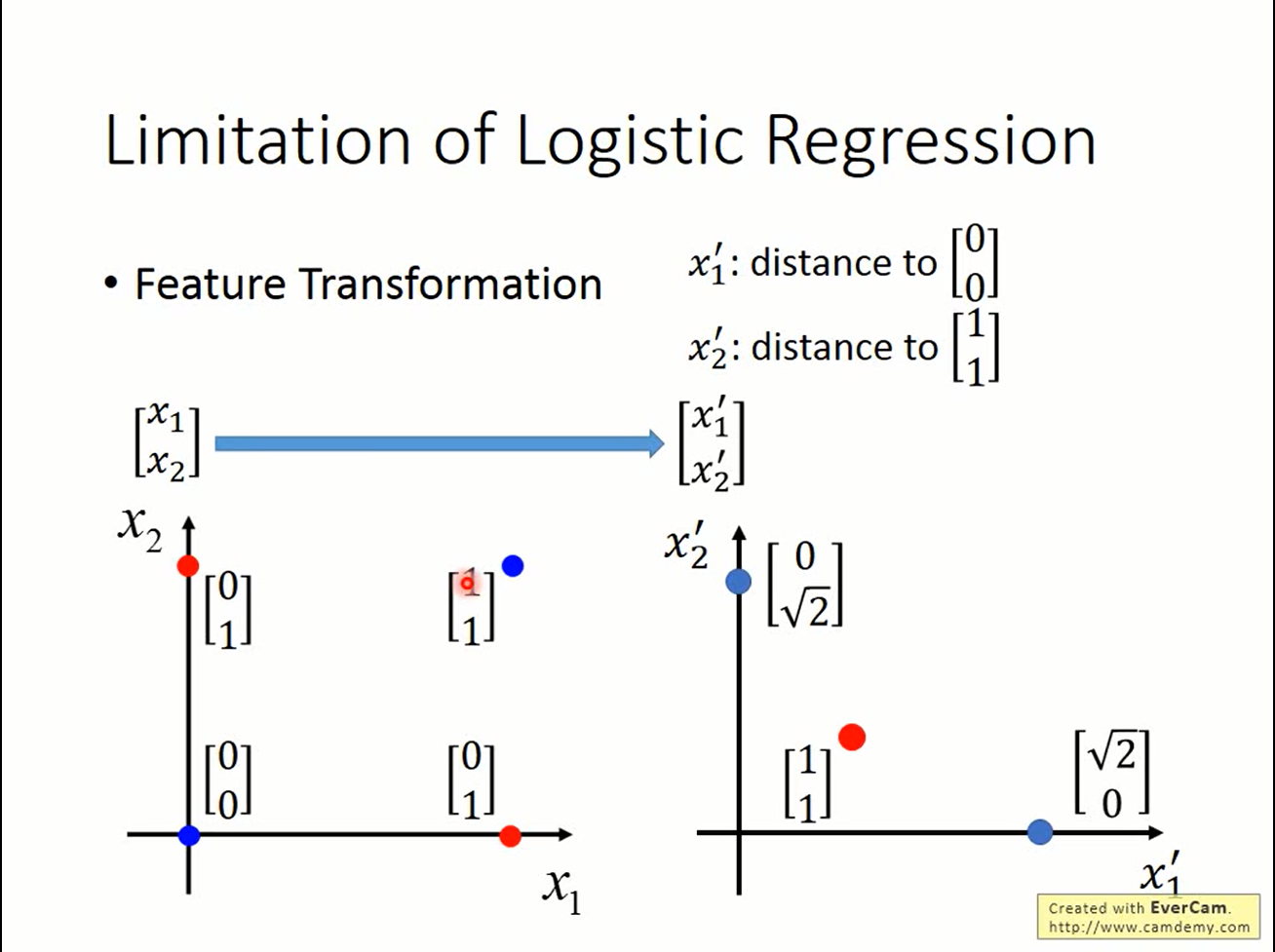
通过对feature做一些处理,是有可能突破线性模型的限制的。 但需要人工参与,而且没有一般规律。这就变成人工学习而不是机器学习了:(
feature transformation with linear unit
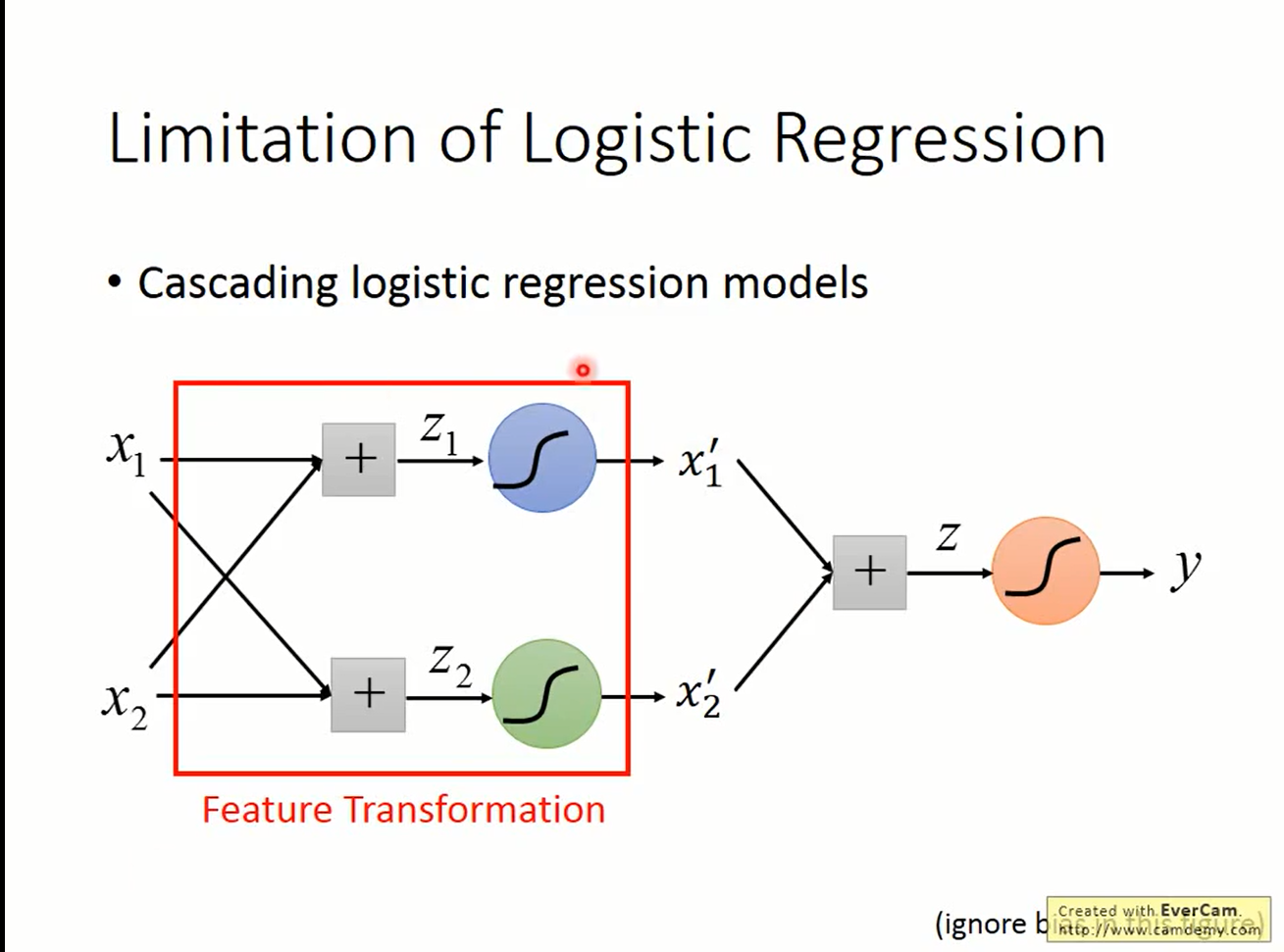 但我们可以把feature transformation看作是一个线性的变化,这样就可以由logistic regression来解决。这样把多个logistic regression串起来,就可以对feature做复杂的变化。
但我们可以把feature transformation看作是一个线性的变化,这样就可以由logistic regression来解决。这样把多个logistic regression串起来,就可以对feature做复杂的变化。
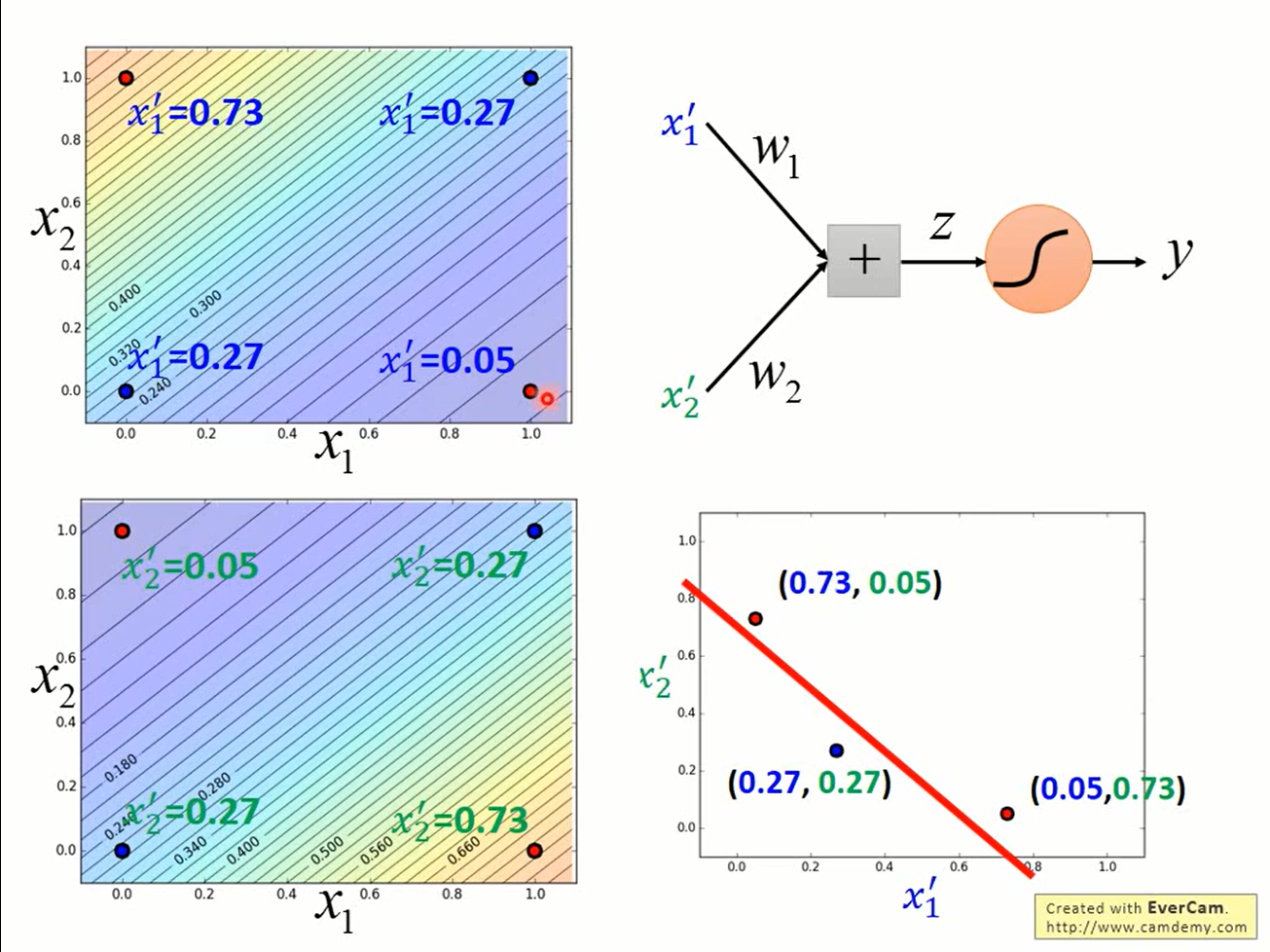 上图是使用两个logistic regression进行feature transformation的结果,只要再接上一个logistic regression接收他俩的输出就可以进行分类了。
上图是使用两个logistic regression进行feature transformation的结果,只要再接上一个logistic regression接收他俩的输出就可以进行分类了。
Neural network
由此推广,把若干个线性模型串起来就可以实现很多复杂的功能。那么给logistic regression的单元起个新名字叫做神经元(neuron),把它们互相连接形成的结构叫做神经网络(neural network),瞬间就高大上起来了。
现在你可以骗麻瓜说「我们在模拟人类大脑的运作实现人工智慧」了;-)