循环神经网络

Machine learning
  1. 1. Why RNN
  2. 2. Vanilla-RNN
  3. 3. Exploding/Vanishing gradients
  4. 4. LSTM

Recurrent Neural network(RNN)是一种专门处理序列的神经网络。正如CNN可以轻易地处理大规模的“网格状”数据，RNN能够处理其他网络架构都无法处理的长的序列。

Why RNN

考虑这样的问题：航空公司要从文字中提取顾客的目的地和出发地。

对于

I’ll arrive from Shanghai to ShenZhen

目的地是ShenZhen，出发地是Shanghai

而对于

I’ll arrive to Shanghai from ShenZhen

则目的地是Shanghai，出发地是ShenZhen。

使用基于地点在句中位置的方法无法解决问题。到底是出发地还是目的地，与前后的词语都有关。这些信息这称为Context(上下文)

若使用MLP，则需要在每个位置都重复的学会人类语言的规则，大量重复的参数不但使得计算代价激增，而且也显著增加over-fitting的几率。

因此，需要一种专门的结构来处理序列数据。RNN应运而生。

Vanilla-RNN

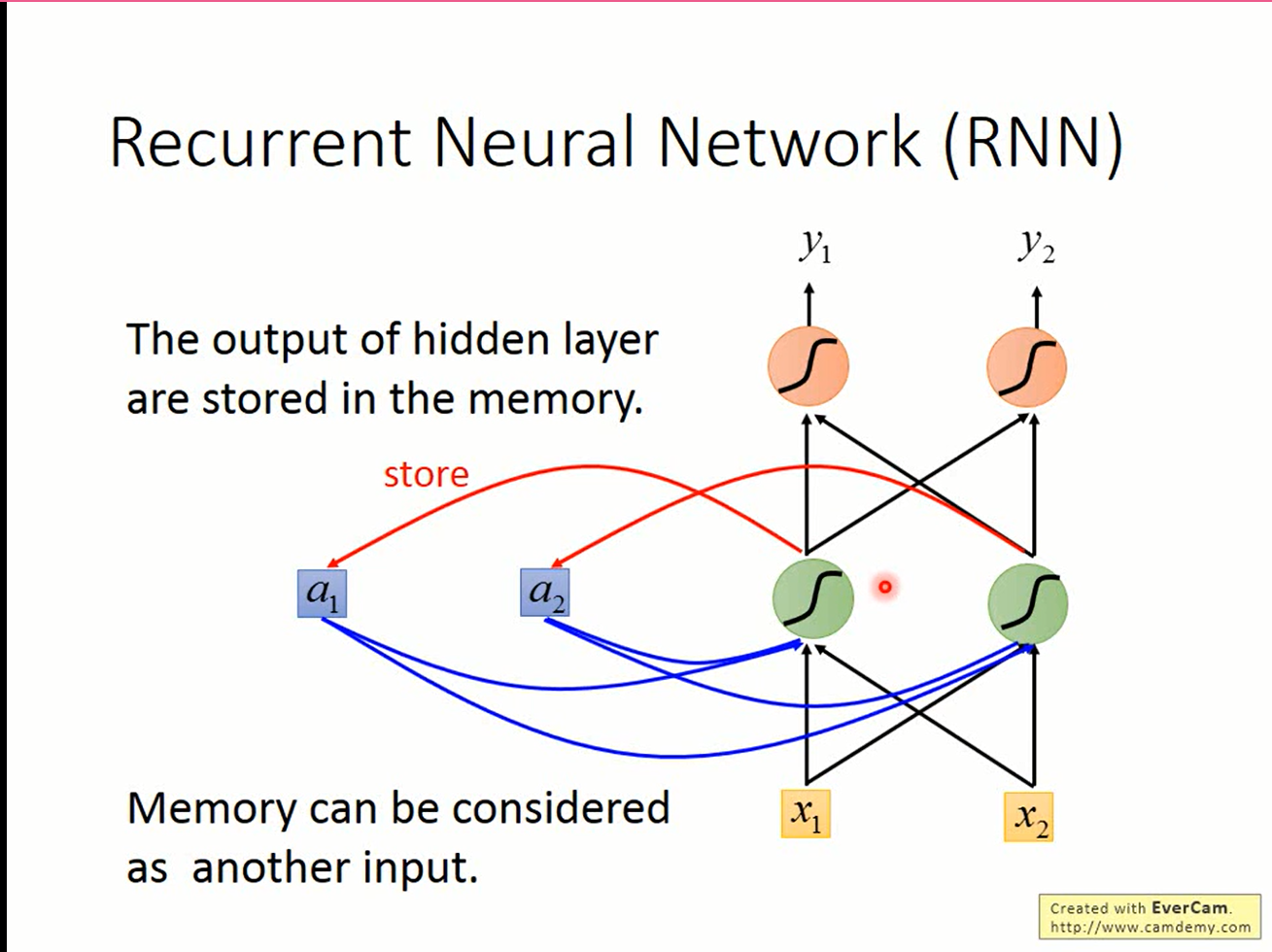
RNN企图使用Memory(记忆)来解决问题：
当前数据处理过程中隐藏单元的值被保留，下个数据处理时作为额外的输入，这样RNN就拥有了“记住”已经看过数据的能力。

Network with memory

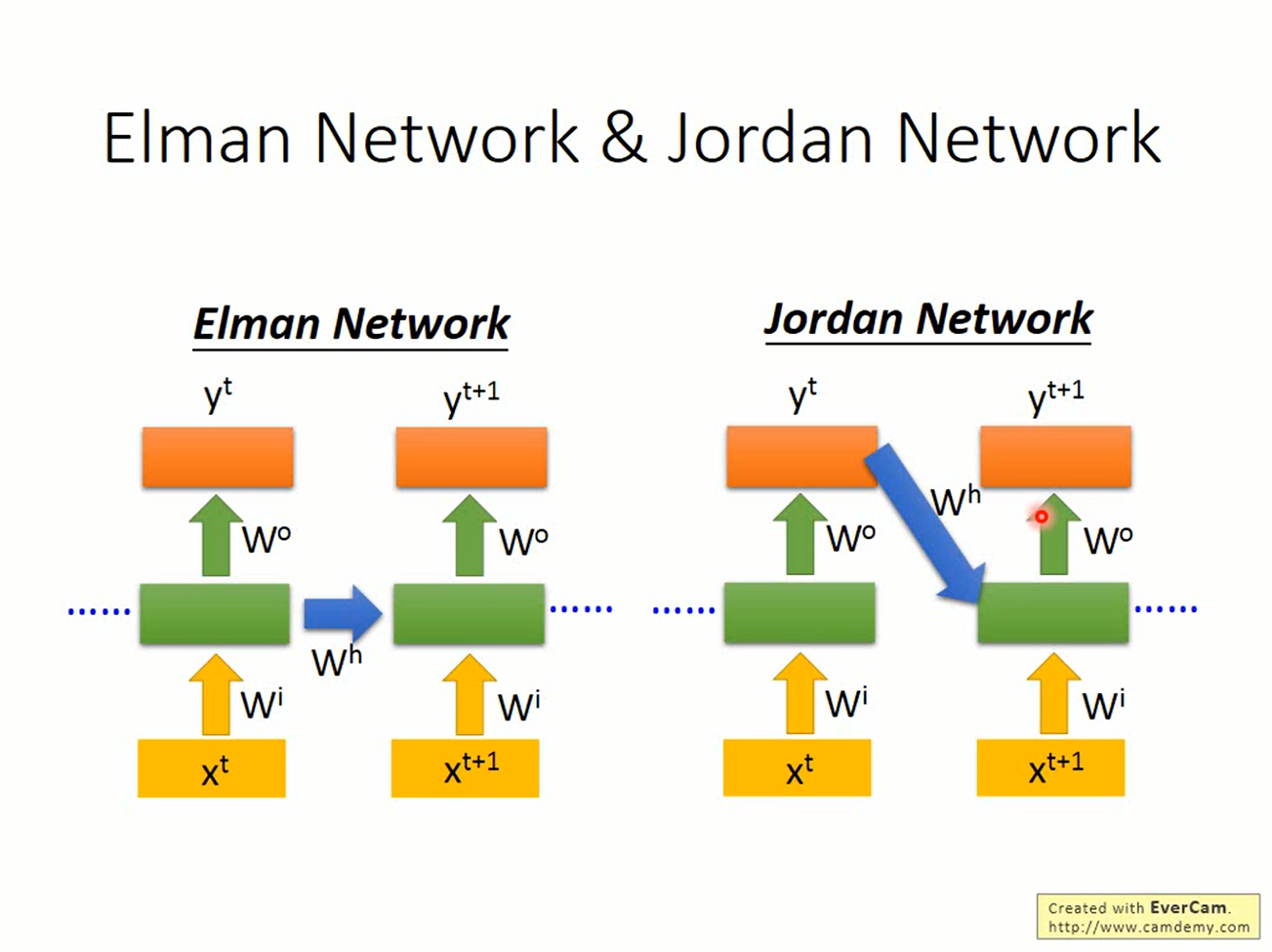
根据“记忆”的来自隐藏单元还是输出的不同，可以将RNN分为Elman network和Jordan network两种
Vanilla RNN

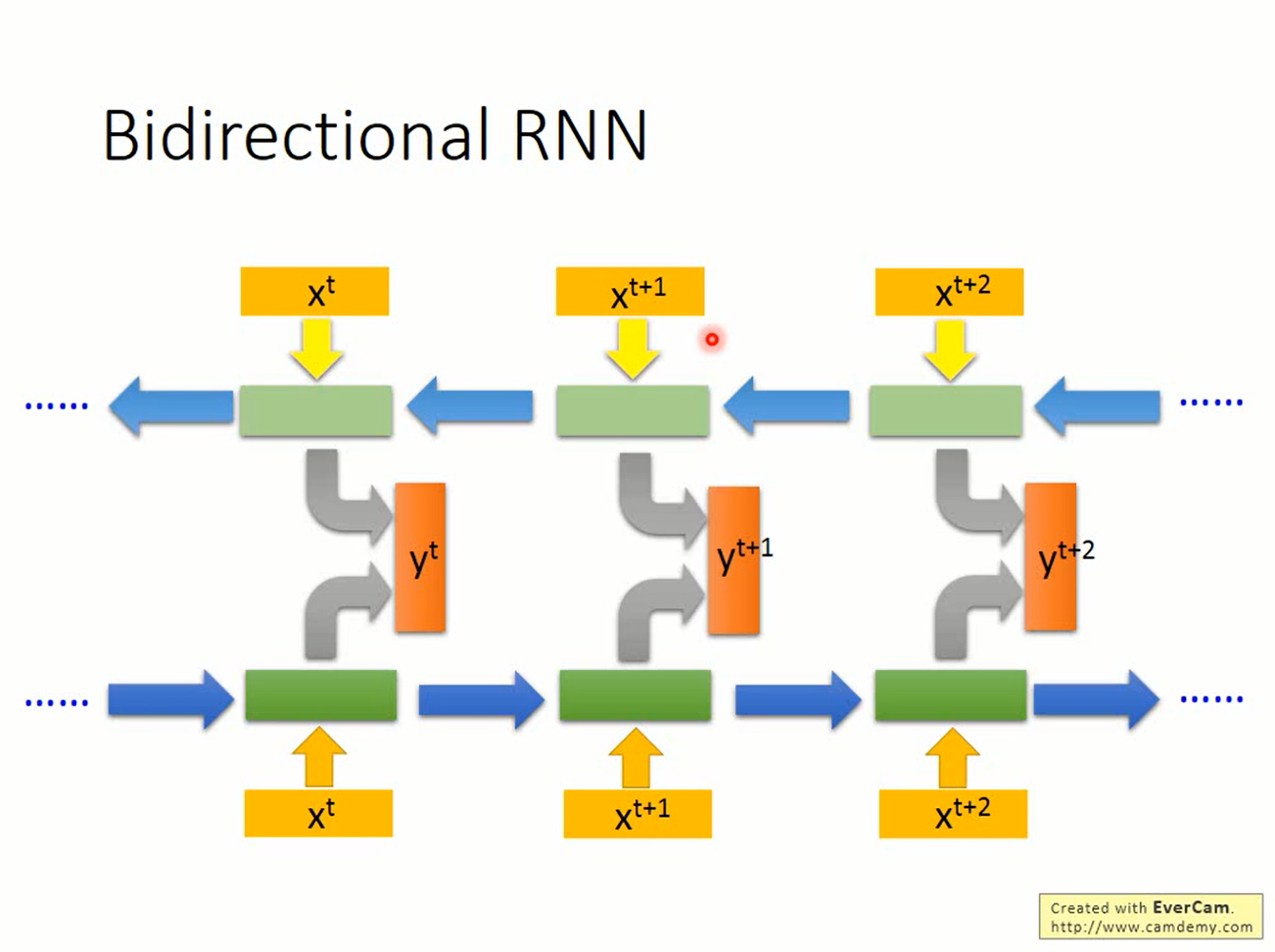
现在的RNN只能往一个方向看，有时只“往前看”的网络并不能解决问题，我们还需要“往后看”。既往前看又往后看的RNN叫做bidirectional RNN(双向RNN)

这时只要训练两个RNN：一个从前往后，一个从后往前，再把他们的输出丢到另一个MLP去做处理就可以了
bidirectional RNN

Exploding/Vanishing gradients

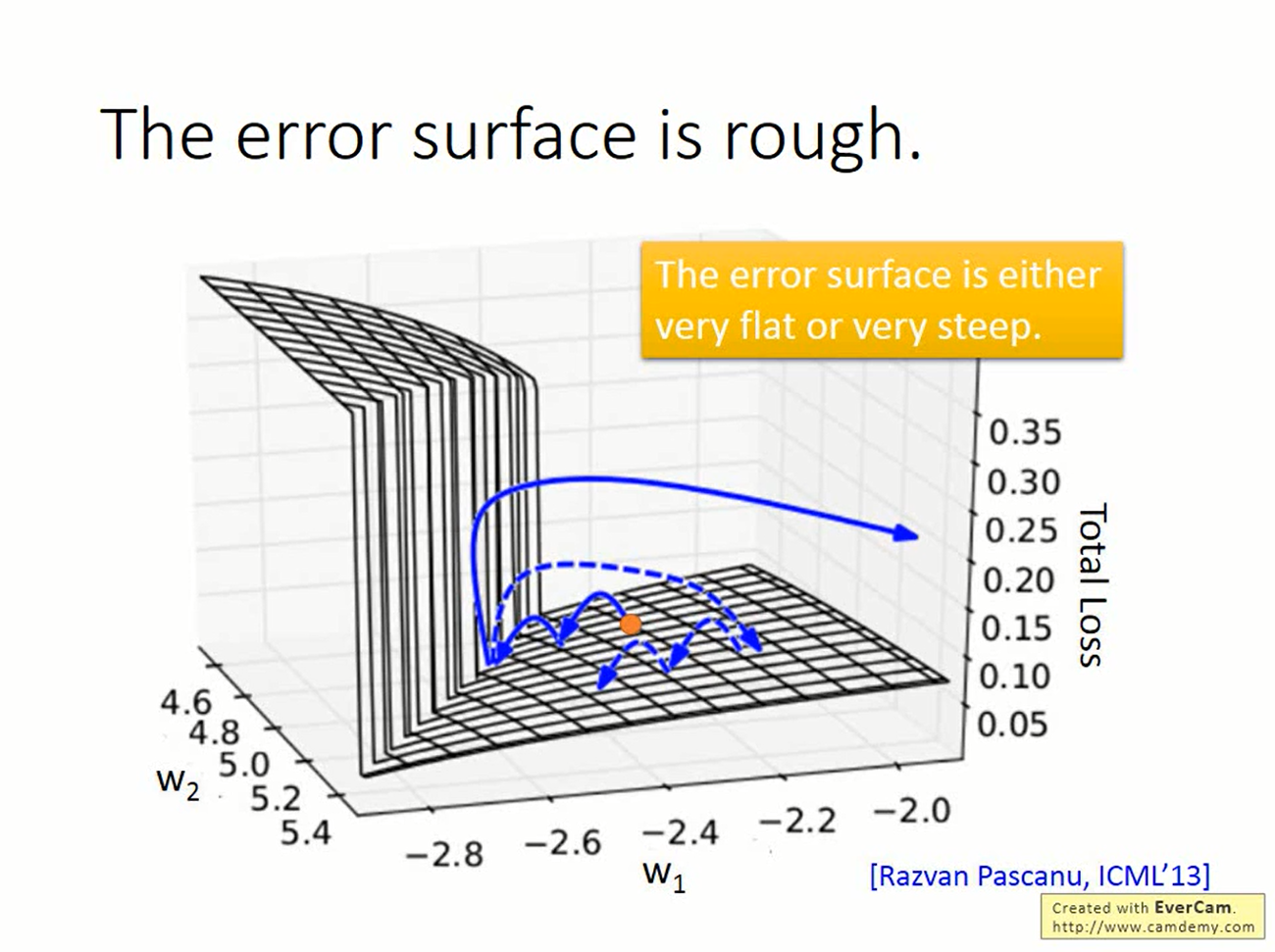
RNN的性能十分出色，但训练的过程往往困难重重。其中一个重要的因素就是Exploding/Vanishing gradients(梯度爆炸/消失)。

exploding-vanishing-gradient
在RNN中，t-1时刻的隐藏单元的输出会影响到t时刻的隐藏单元。

重复使用这个式子，则

若W可进行特征值分解，则

  • 若W的特征值λ>1，则经过t次相乘后，λ^t的值会变得非常大(梯度爆炸)。
  • 若λ<1，则经过t次相乘后，λ^t的值会变得非常接近零(梯度消失)

梯度爆炸/消失对梯度下降法的干扰非常大，以至于训练过程中出现匪夷所思的结果
匪夷所思

解决这个问题的关键在于给“记忆”可变的权重。

LSTM

Long short-term memory(长短期记忆)是一个解决梯度爆炸/消失问题效果较好的方案。
LSTM
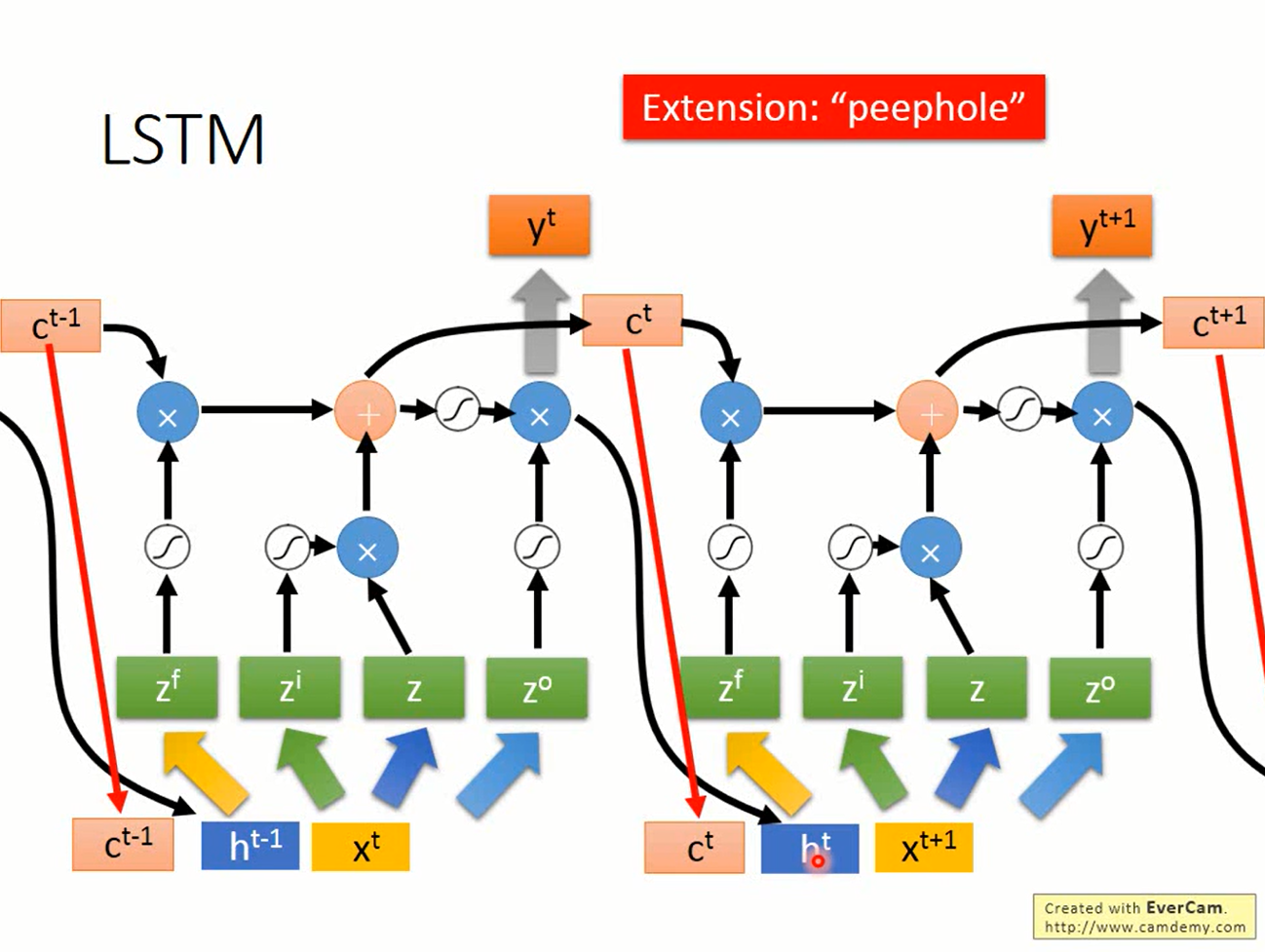
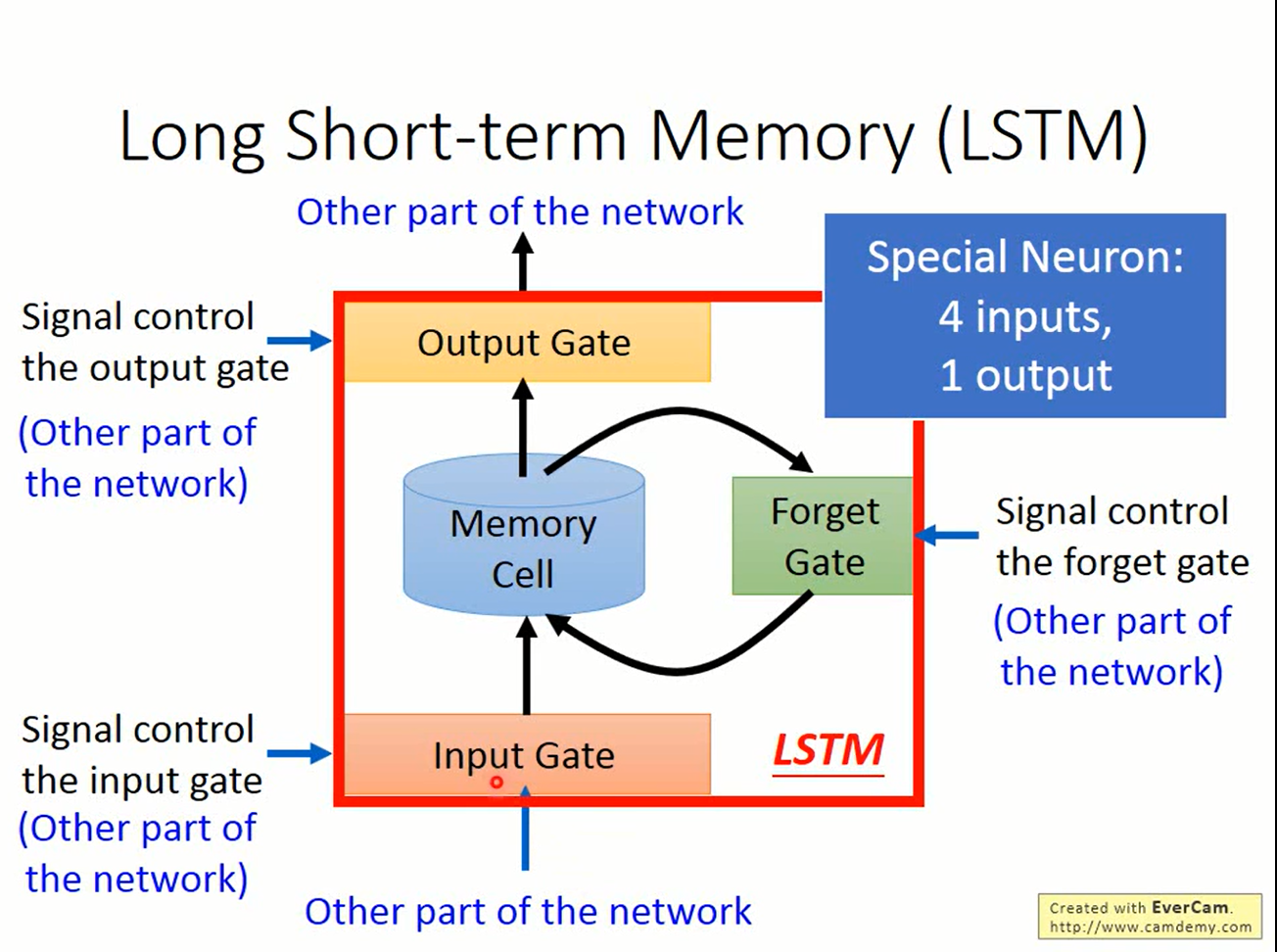在LSTM中，在存储“记忆”的地方(cell)加上了三个gate：

  • input gate
  • output gate
  • forget gate

这些gate的控制信号经过sigmoid函数后得到的0~1之间的数值表示这些门“打开”的程度

  • input gate决定“记忆”是否接受新的输入
  • output gate决定“记忆”是否被读出
  • forget gate决定“记忆是否被遗忘”

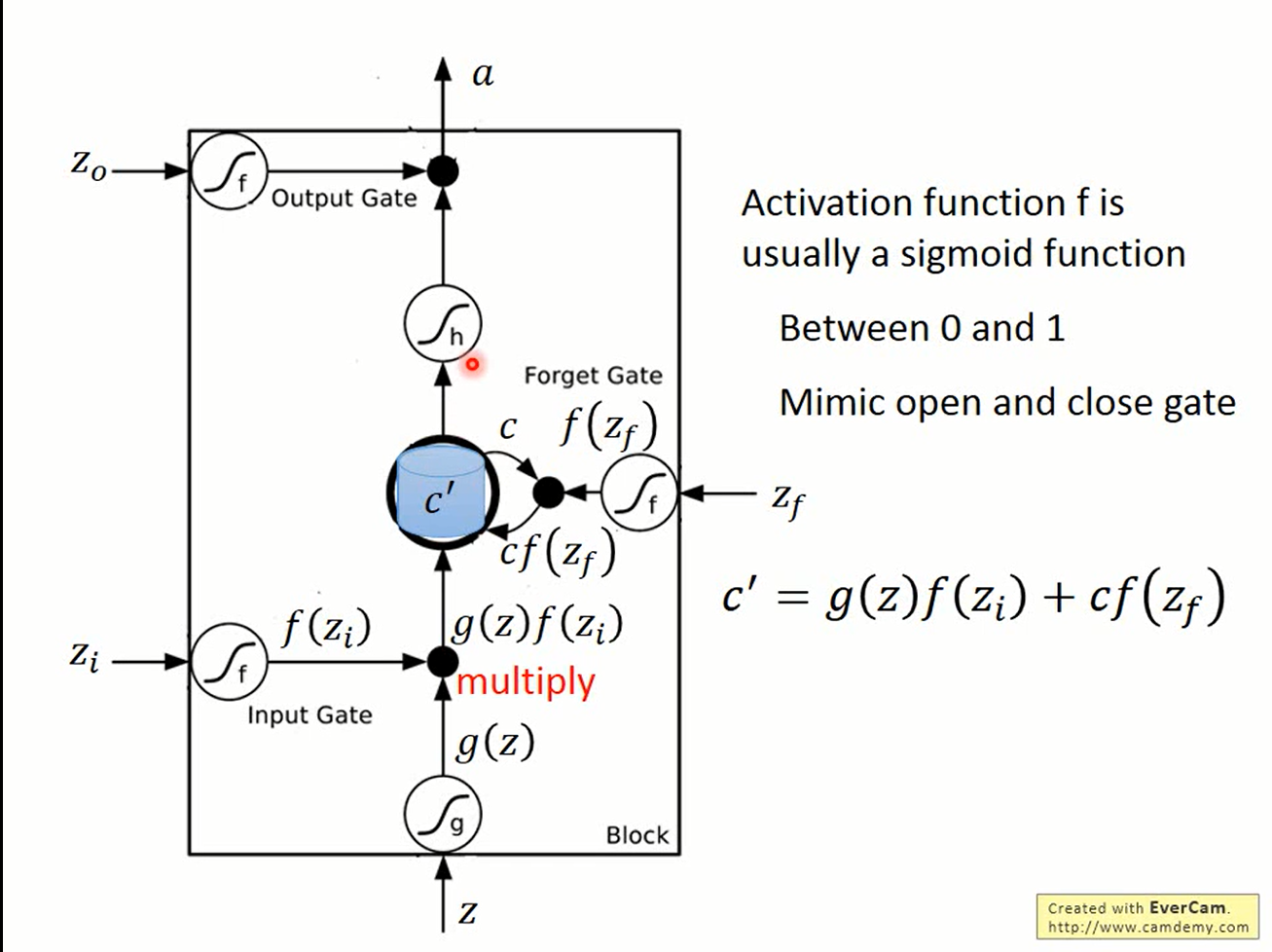
LSTM cell

图中z是输入,zi,zo,zf分别是上述三个gate的控制信号。
设原来存储在“记忆”中的值为c,则新的值c’如此产生

  1. 输入z经过激活函数的值g(z)与input gate的值相乘，得到g(z)*f(zi)
  2. 原来“记忆”中的值c与forget gate的值相乘得到c*f(zf)
  3. 将输入与原“记忆”相加的结果作为新的记忆c’=g(z)f(zi)+cf(zf)
  4. 新的值c’与output gate的值相乘得到c’*f(zo)，结果作为“记忆”的输出

其中zi,zo,zf是网络的参数，由训练过程中自己学得。将多个LSTM的cell连接起来，就得到了能够处理复杂问题的RNN。当然在实际使用中，zi,zo,和zf也可以接受网络其他部分的参数
，这就要看具体的问题了。

Deep-LSTM.png

Machine learning RNN
prev： next：