前言
主成分分析(Principal component analysis,PCA)是一种常用的无监督学习算法。经过PCA后的数据会在它所处理的维度上会不相关(decorelation)。 而PCA所选的维度又通常比本来的维度要小,因此也可以用来做降维处理。
PCA
PCA的想法很朴素。它试图找到一个线性变化W,使得经过变化后的向量z=Wx在各个维度z_i上都拥有最大的方差。
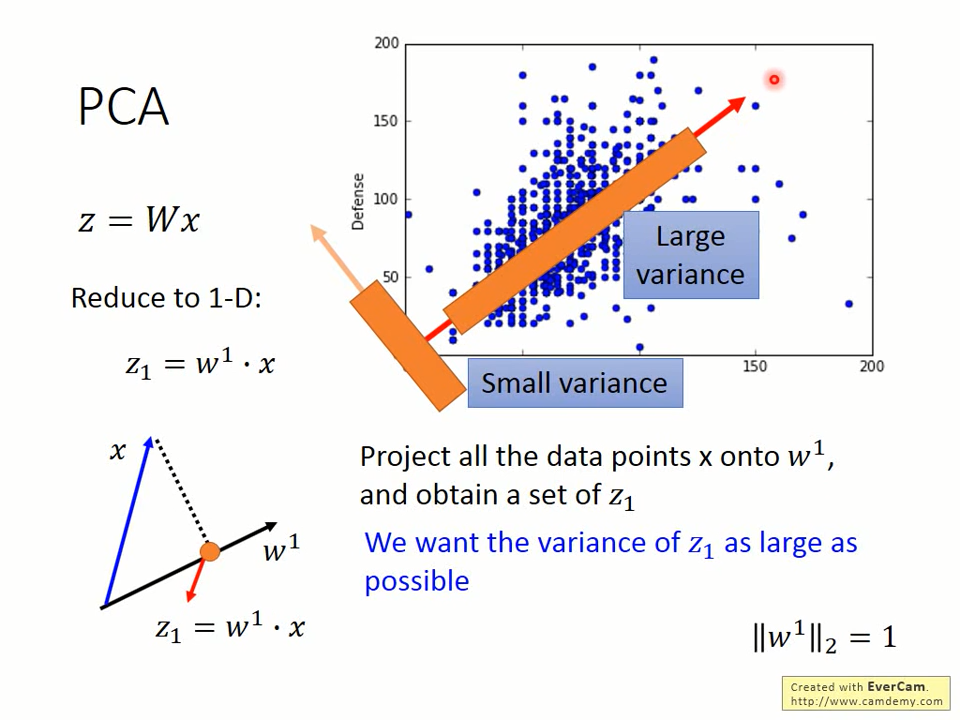
Constraints
仅仅要求方差最大而不做任何限制是不行的。我们总是可以让w_i含有无穷从而使方差变为无穷大,但这没有意义。
因此限制w_i的模是1。
同样的,当找出使得第i维的方差最大的参数w_i后,机器可以把这组参数w_i用在第j维上来“偷懒”,因此限制任意的参数是垂直的。
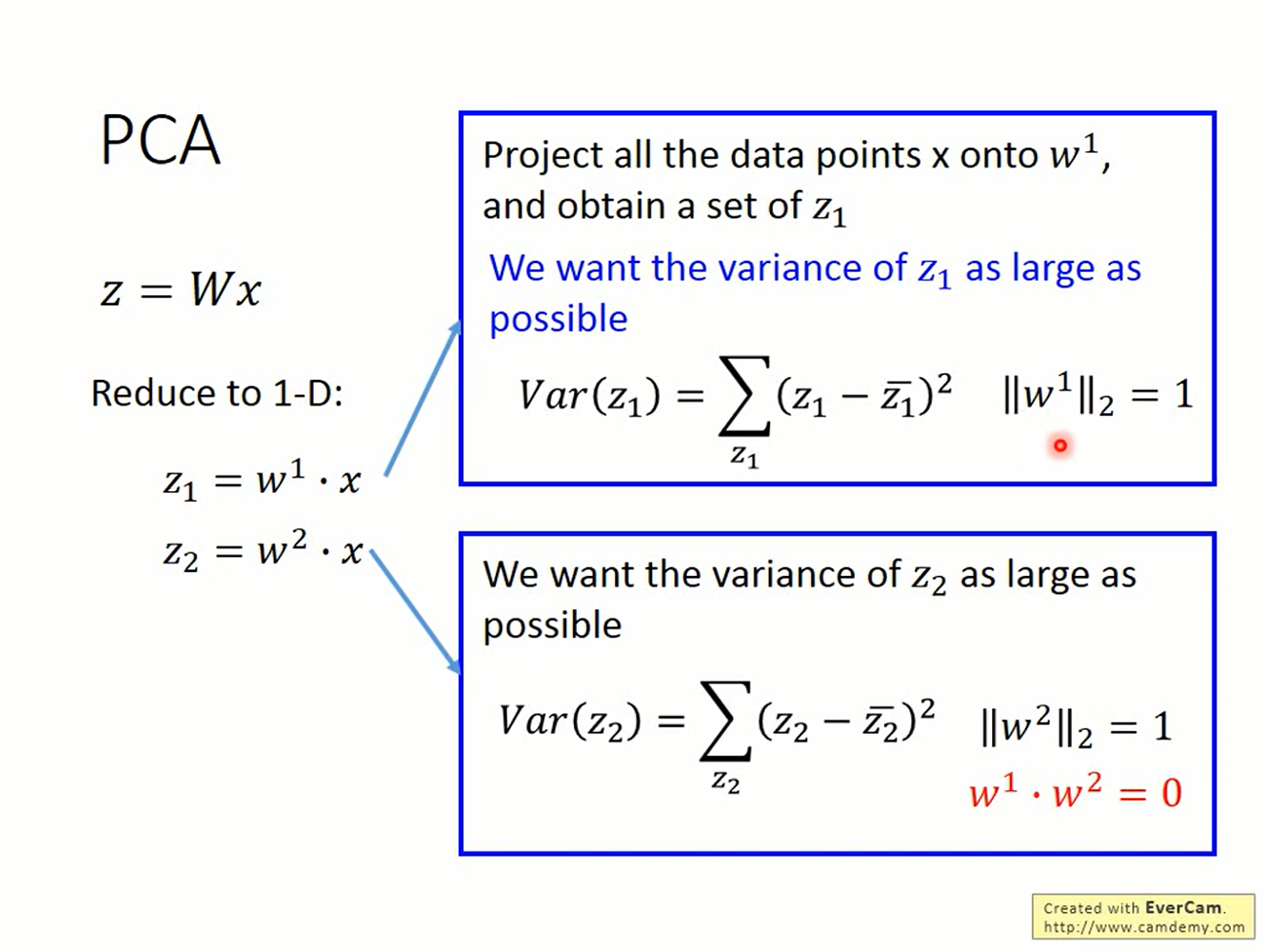
Dimension reduction
to 1 dimension
先考虑一维的情况。
$$ z_1=w_1'x,其中 (w_1')^\top w_1'=1 $$

构造拉格朗日函数,其中S=Cov(x),
$$ L(w_1')=(w_1')^\top S w_1'-\alpha((w_1')^\top w_1'-1) \\ \frac{\partial L}{\partial w}=0 \rArr Sw_1'-\alpha w_1' \rArr Sw_1' = \alpha w_1' \rArr \alpha是S的特征值,w'是对应的特征向量 $$带回到上式
$$ (w_1')^\top\mathrm{Cov}(x)w_1' = (w_1')^\top Sw_1' = (w_1')^\top \alpha w_1' = \alpha (w_1')^\top w_1'=\alpha $$
α的最大值,即是Cov(x)最大的特征值。此时的w1'为α对应的特征向量
对于二元的情况也类似
to 2 dimensions

拉格朗日函数
$$ g(w_2)=(w_2')^\top S w_2 - \alpha((w_2')^\top w_2' = 1) - \beta((w_2')^\top w_1') $$而
$$ (w_2')^\top w_2' = 1 \\ (w_1')^\top w_2' = 0 \\ (w_1')^\top Sw_2'=((w_1')^\top Sw_2')^\top =(w_2')^\top S^\top w_1 \\ =(w_2')^\top S w_1 = (w_2')^\top \alpha w_1 \\ =\alpha (w_2')^\top w_1 = 0 $$
所以系数拉格朗日函数的只剩下β.
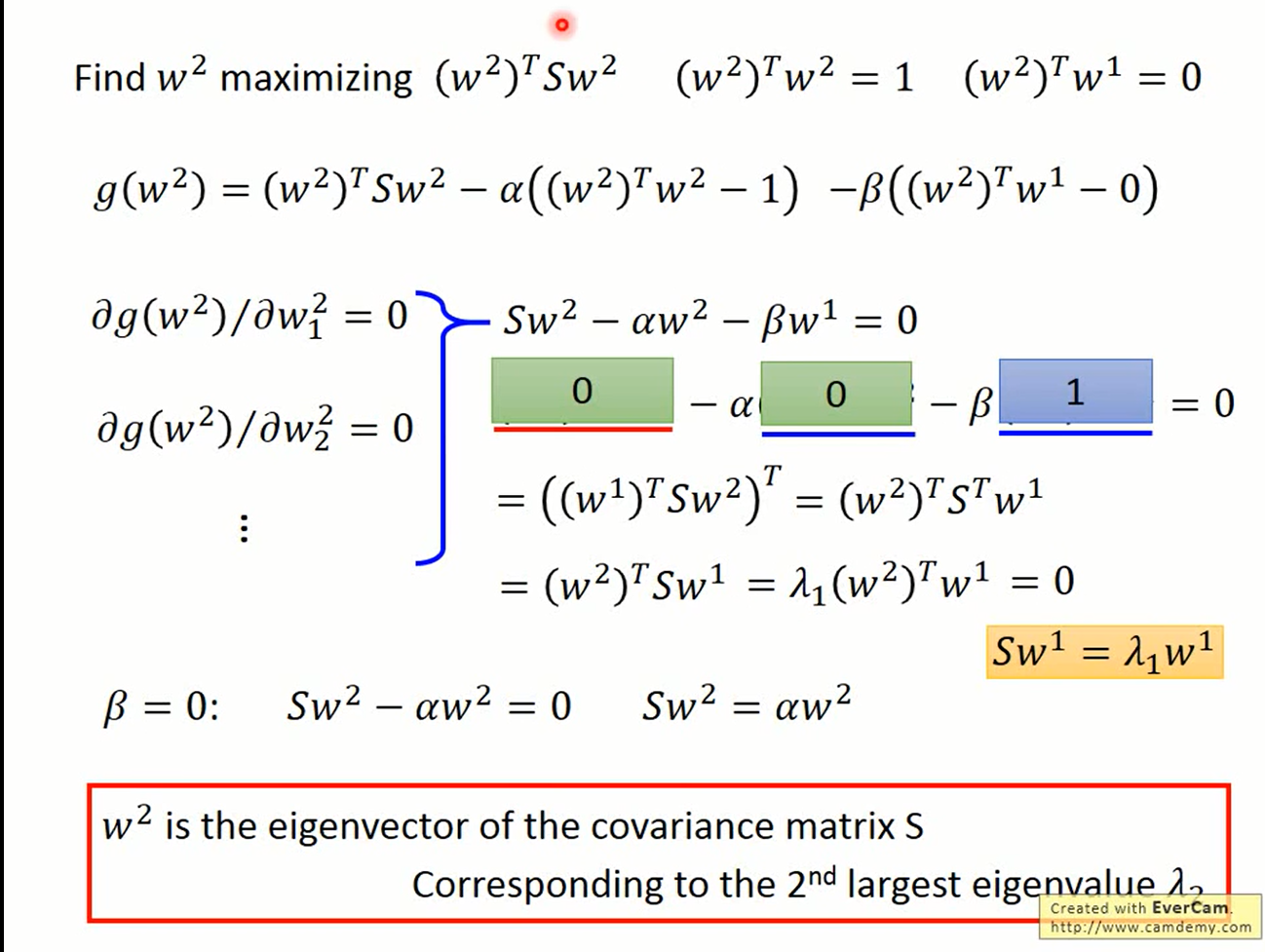
β的最大值,即是Cov(x)第二大的特征值。此时的w2'为β对应的特征向量
to k dimensions
把PCA推广到k维,则W是Cov(X)的最大的k个特征值所对应的特征向量的行矩阵。
Decorelation
PCA处理后的z矩阵的各个维度之间是没有相互关系的。

将W展开,
$$ Cov(z)=WS\left[w^1,w^2...w^k\right] $$$$
=W\left[Sw^1,Sw^2…Sw^k\right]
$$ $$=W\left[\lambda_1w^1,\lambda_2w^2…
\lambda_kw^k\right]
=\left[w^1,w^2…w^k\right]^\top \left[\lambda_1w^1,\lambda_2w^2…\lambda_kw^k\right]
$$ $$\forall i, (w^i)^\top w^i = 1
$$ $$\forall i\not ={j}, (w^i)^\top w^j = 0
$$ 因此 $$Cov(z)=diag(\lambda_1,\lambda_2,…,\lambda_k) $$ 协方差矩阵为对角阵,所以不同分量之间没有线性的相关性。