前言
支持向量机(Support Vector Machine,SVM)是一个能求解通用二元分类问题的模型。SVM使用Kernel trick，使得自己在能够表示非线性函数的同时Loss是有闭式解的Convex function。也有人把SVM当作线性模型向神经网络过渡的中间阶段。
SVM
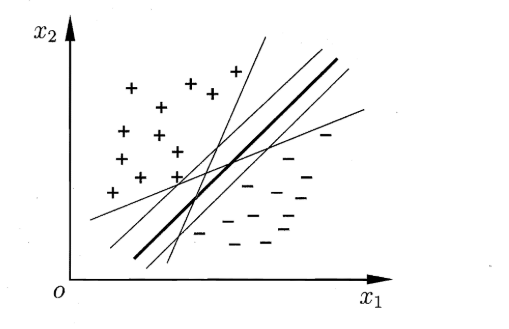
对于 $$ D = {(x_1,y_1),(x_2,y_2)…(x_n,y_n)} , y_i \in {-1,+1}
$$
的分类问题，SVM试图在n维空间上找一个超平面，wx+b，使得
- 当wx_i+b≥1时，yi=+1
- 当wx_i+b≤1时，yi=-1
并且超平面应该离两侧最近的点都尽可能远。解出这一组w和b就解出了SVM。
其实如果在将w和b并在一起作为新的w,将x后接1,则SVM可以进一步简化为wx:
Hinge loss
回到分类问题本身，通常Loss会选择在整个训练集上分类错误的次数：
$$ L(f)=\sum_i \delta(g(x^n) \not ={\hat{y}^n}) $$
其中δ函数的为真时值为1，反之值为0。
正如对率回归中所说，
在分类问题上使用这类函数是不利于训练的，因此希望找到一个函数
来近似代替δ函数。
hinge loss就是这样的一个函数。他是这么定义的：
$$ l(f(x^n),\hat y^n)=\max(0,1-\hat y^nf(x)) $$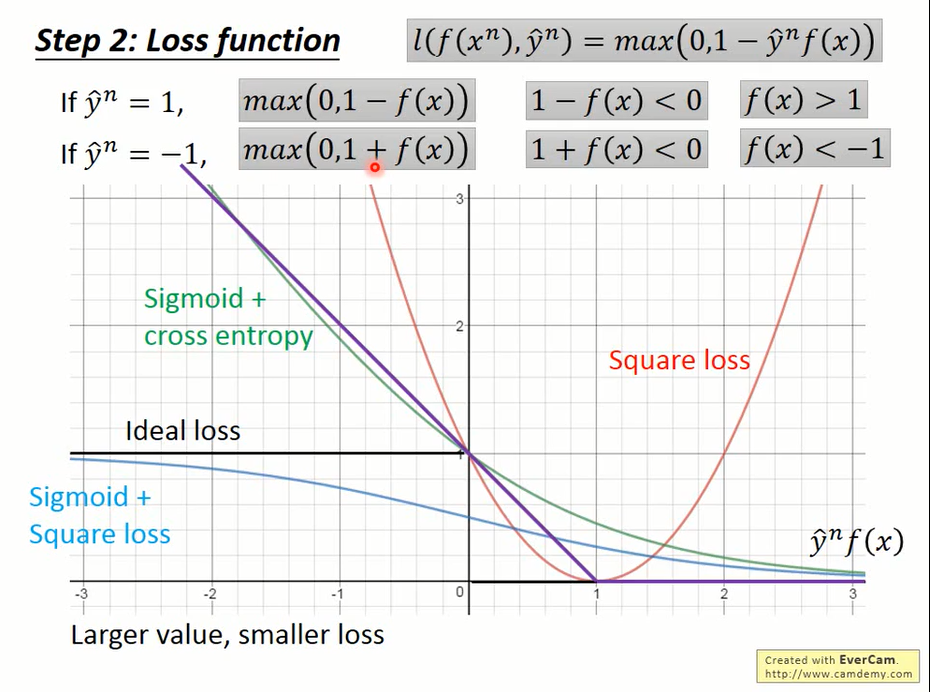
图中紫色的线就是hinge loss。横坐标1处，hinge loss把两条直线连接起来，就像是连接骨头的关节(hinge)，因此得名。
从图上可以看出
- MSE随着横坐标的增加loss反而增加，根本不适用
- sigmoid+square loss对横坐标的变化不敏感(saturate)，训练起来也不好做
- sigmoid+cross entropy会积极的将坐标点往右推，但其实只要横坐标超过了1就已经足够了
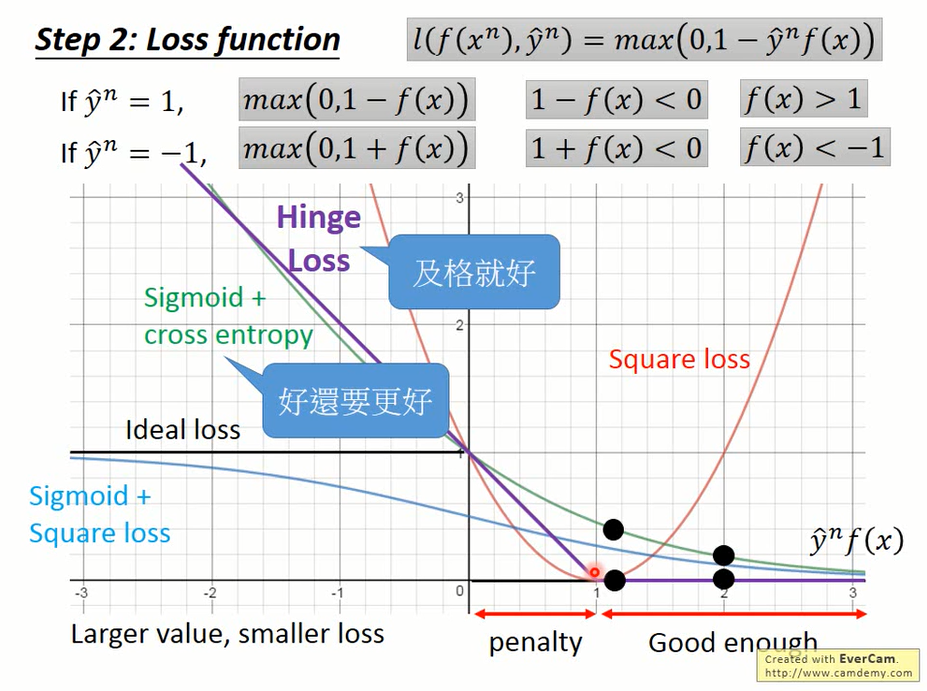
cross entropy好像完美主义者，而hinge loss会想着及格就好。既然在现实世界里两者的性能是一致的，我们也就乐得省下这些无畏的开销。
Gradient descent
hinge loss对w的偏微分后，得到梯度下降的公式
$$ w_{i+1}=w_i-\eta\sum_n c^n(w)x_i^n $$其中
$$ c^n(w) = -\delta(\hat y^nf(x^n)<1)\hat y^nx_i $$soft margin
将整体的损失函数L
$$ L(f)=l(0,1-\hat y^nf(x)) + \lambda|w|_2=\sum_n \max(0,1-\hat y^nf(x)) + \lambda|w|_2 $$
中的l用ε代替，得到下列形式
而不是硬性规定
$$ \hat y^nf(x) \ge1 $$
ε作为边界条件的放松，被称作松弛变量(slack variable)
Support vector
SVM的w是所有训练样本点的线性组合，并且多数点的系数都是0(sparsity)。
这个性质可以从KKT系数反映出来
当然，它也可以从另一个角度说明。
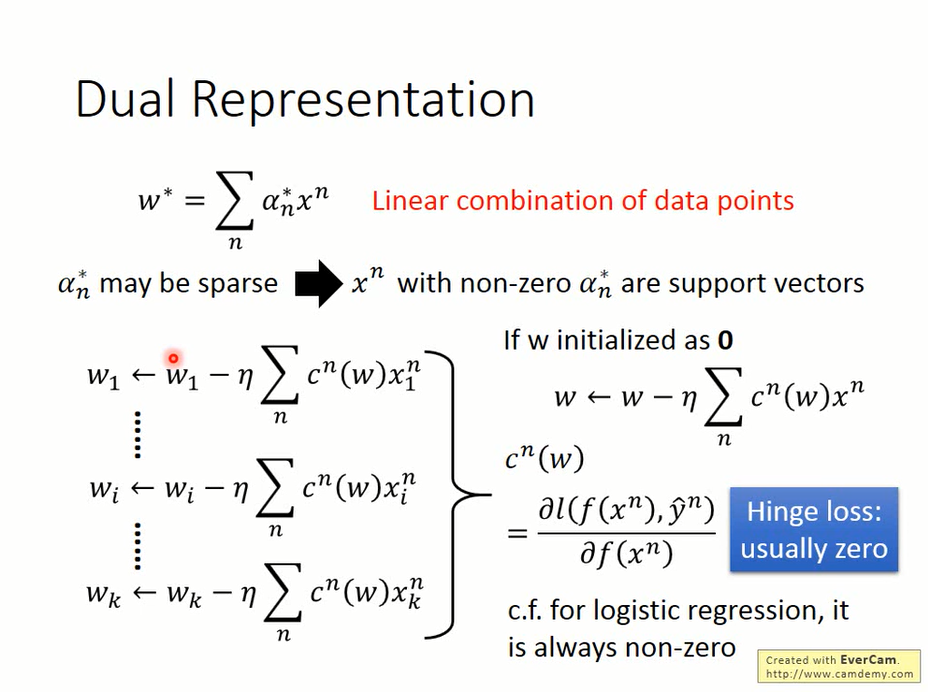考虑梯度下降的式子
其中
$$ c^n(w) =\frac{\partial l(f(x^n),\hat y^n)}{\partial f(x^n)}=-\delta(\hat y^nf(x^n)<1)\hat y^nx_i $$当w被初始化为0向量时，每一次参数更新加上了一个样本点的线性组合；而hinge loss有大约一半的定义域里微分是0，因此大部分系数会为0
Kernel method
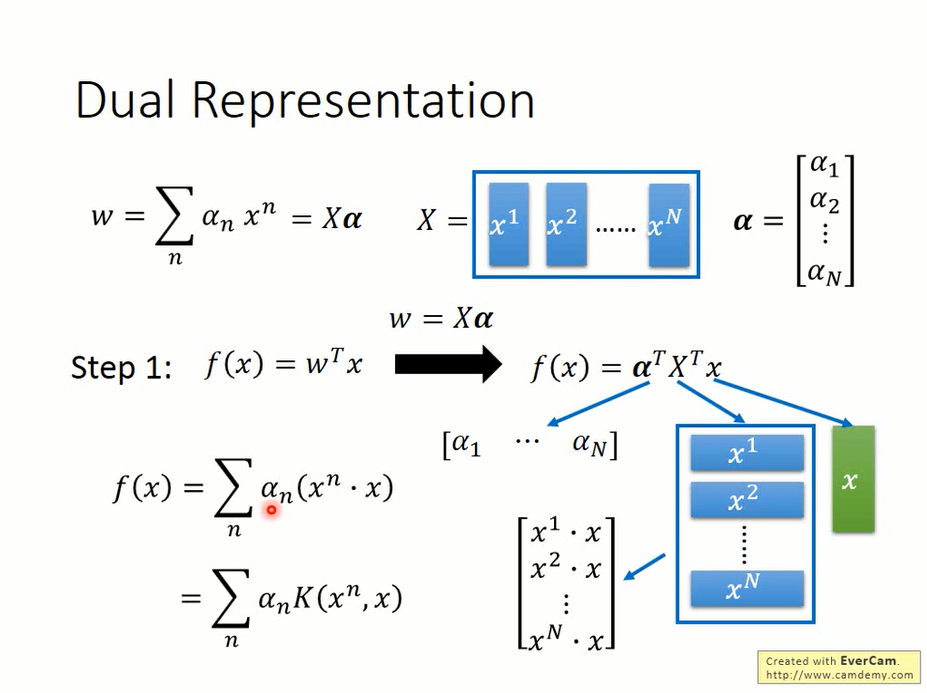
既然w是X的一个线性组合，将其写作w=Xα。
带入f(x)
将x^n与x的内积用函数K(kernel function)表示，则
$$ f(x)=\sum_n \alpha_nK(x^n,x) $$
将得到的f(x)带入loss，发现L(f)与x已经无关了，可以直接进行梯度下降。这就是Kernel trick
若我们先对x做feature transform φ(x)，φ(x)·φ(z)有时可以表示为K(x,z)。这即扩展了SVM的表述能力，也提高了效率。
在使用RBF Kernel时，可以在无穷维空间做内积
SVM and Neural network
SVM也可以被看作是有一层hidden unit的神经网络:
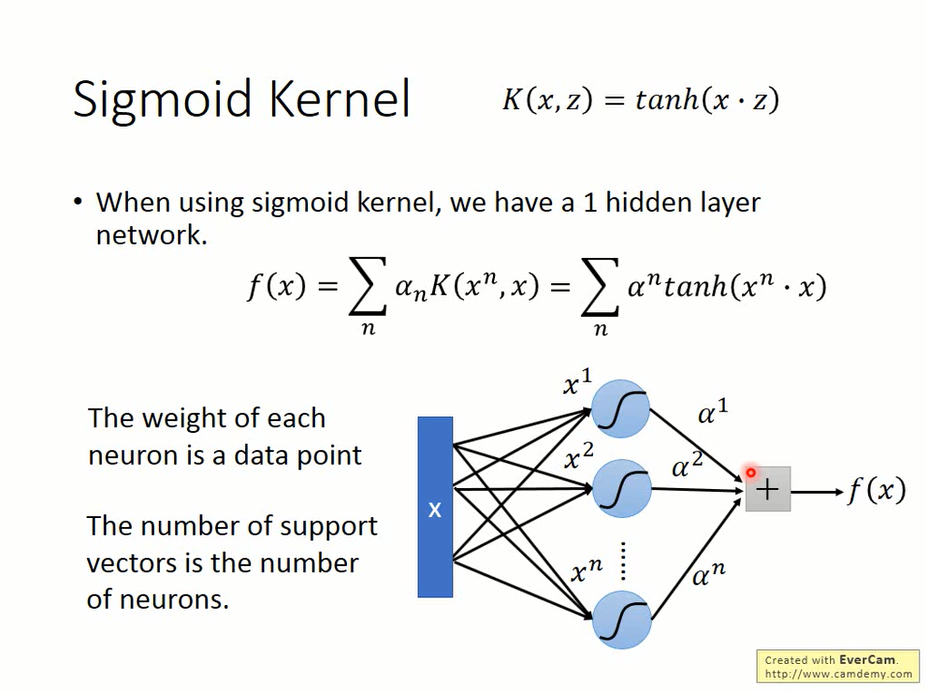
每一个neural的weight是x^n与x的内积，所有neural的输出经过tanh后再以α为权值求和就得到输出了。
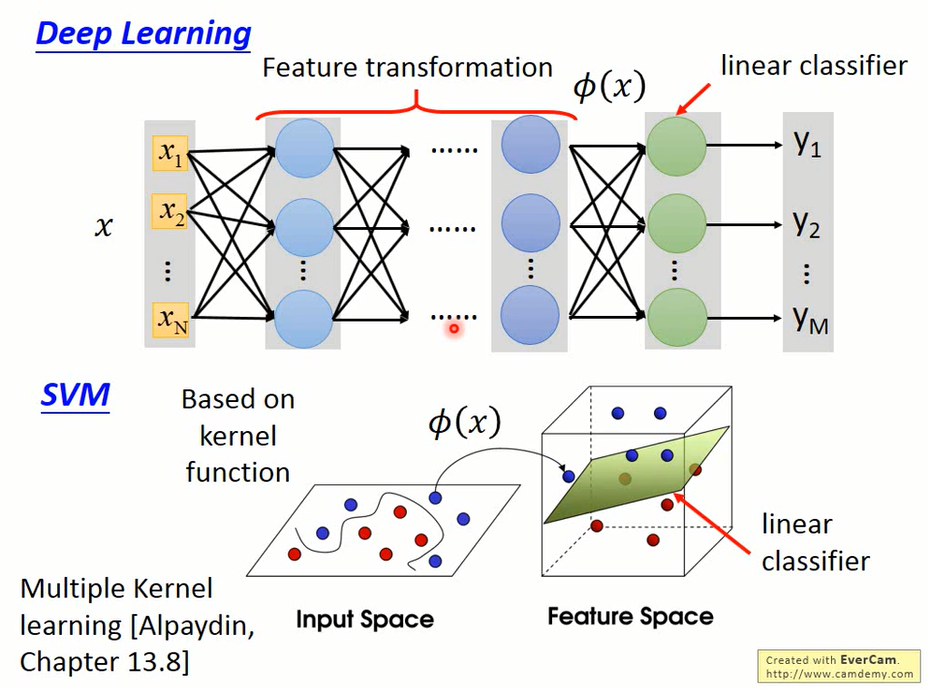实际上，SVM也可以看作是一个神经网络。
- Kernel function相当于是神经网络中做feature transform的hidden layer
- SVM学到的分类器与神经网络的输出层学到的分类器是一致的。