前言

本文的是台湾大学2020机器学习Semi-supervised leraning的笔记。奉行Lazy evaluation策略，对这些知识更深层次的探究只在绝对必要时完成。

现在是所谓的大数据时代，每人每天产生的数据成千上万。对商业公司来说，数据的收集已经不是问题，但给数据添加标记的工作因为其所需要消耗的人力物力成为老大难问题；而在机器学习中，带标记数据的不足会给模型引入bias。一个很自然的想法是，能不能用这些不带标记的数据来提高模型的泛化性能呢？答案是肯定的。这就是半监督学习。

在半监督学习中，数据分为两块。

$${(x^r,\hat y^r)}_{r=1}^R,{x^u}_{u=R}^{R+U}$$

其中R是带标记数据(labeled data)的数量，U是不带标记数据(unlabelled data)的数量。U通常远远大于U；
根据testing data是否包括unlabelled data，可将半监督学习分为两类。

半监督学习为什么有效，一个比较令人接受的说法是，无标签数据的分布对问题有些启发。
而半自动学习有没有用，有多大用，取决于假设做的好不好；

Semi-supervised Learning for Generative Model

在二元分类时，曾经用过生成模型解决这个问题。

在半监督学习中，分类依旧可以用生成模型来解决。

大体的的思路是，使用unlabelled data来修正对prior的估计，以期更小的泛化错误

具体算法如下:

1. 初始化参数θ
2. 对unlabelled data计算其属于某一个类别的后验概率
3. 更新参数θ: $$P(C_1)=\frac{N_1+\sum_{x^u} P(C_1|x_u)}{N} \\ \mu^1=\frac{1}{N_1}\sum_{x^r \in C_1}x^r+\frac{1}{\sum_{x^u}P(C_1|x^u)}\sum P(C_1|x^u)x^u$$ 算法最终会收敛，但初始化的参数值θ会影响结果。

在监督学习的时候，最大似然函数的结果是有闭式解的；
而在半监督学习时，unlabelled data对应的似然函数依赖于当前参数θ，所以只能迭代的来求解。

---

半监督学习通常基于两个假设

• Low-density Separation Assumption
• Smoothness Assumption

这两个假设成立不成立，对半监督学习的效果息息相关。

Low-density Separation Assumption

Low-density Separation Assumption认为，在分界线上，数据的密度是低的。换言之，这个世界是非黑即白的。

在投影中，左边分界线位置的密度比右边分界线上的密度更低，因此认为左侧分界线更好。

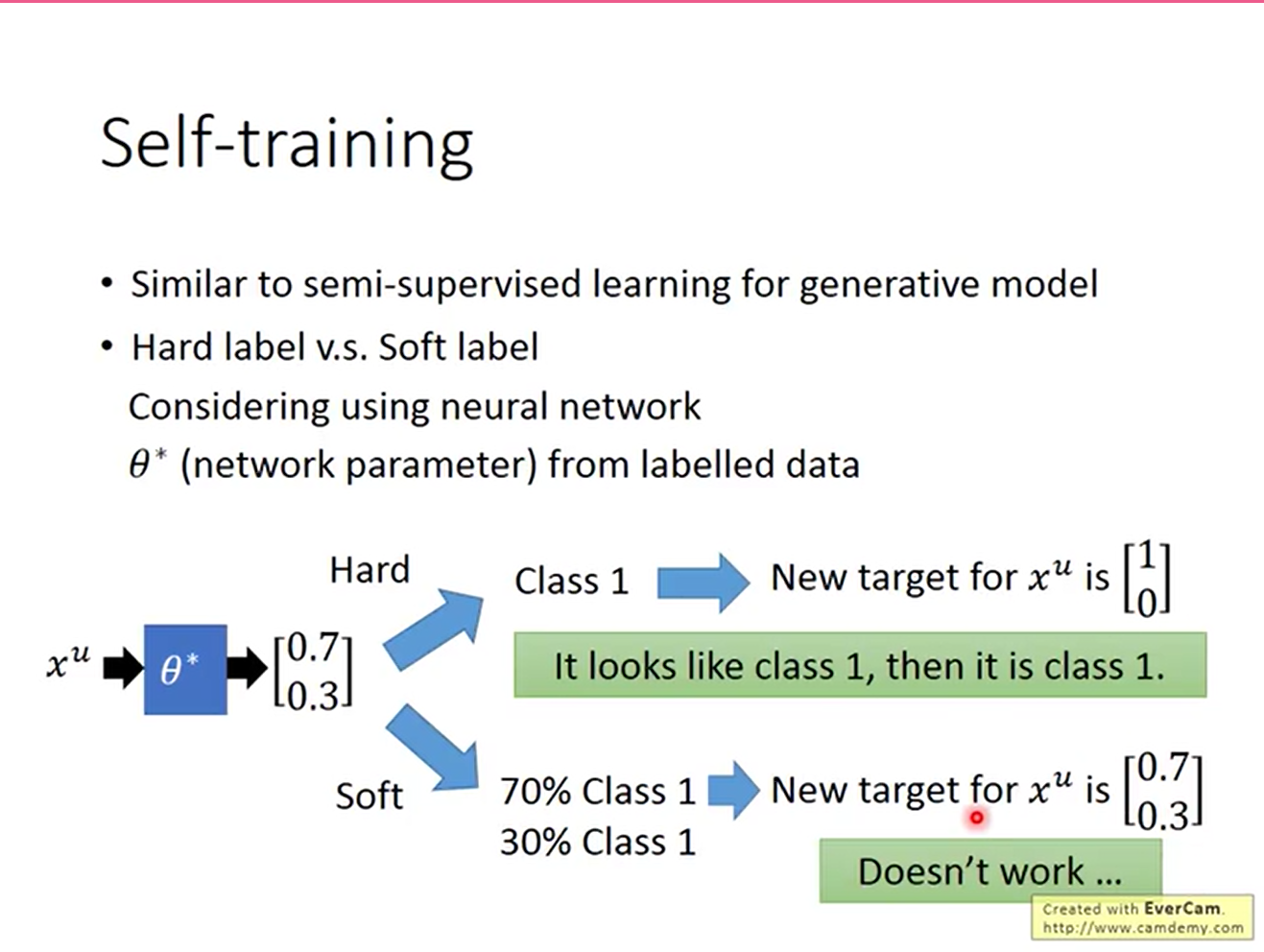
基于这个想法，我们可以提出Self training算法：

1. 根据labelled data训练一个model
2. 用1中得到的model给一部分的unlabelled data打上标记,作为labelled data。这个标记叫做pseudo label(伪标记)
3. 回到1

需要注意的是伪标记是否对新训练的model有用。

如果做regression，pseudo label并不能让model学到新东西，所以就完全没有用处。

如果用神经网络做分类，用soft label也没有用处

换一种思路，我们也可以把Low-density Separation Assumption当作一个regularization term:

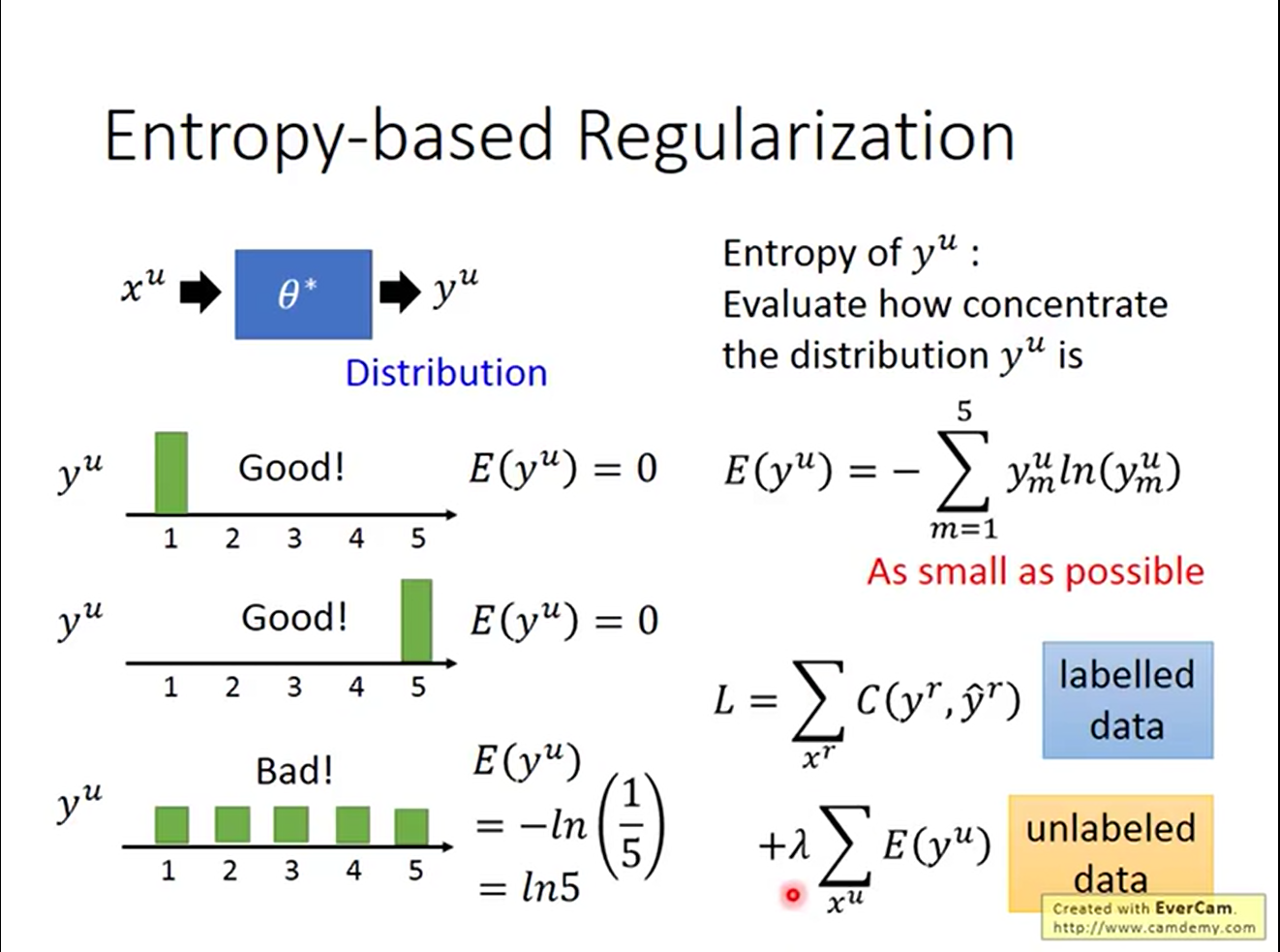
对于一个概率分布，我们希望密度越集中越好。概率分布的集中程度可以用香农熵来衡量。这样把香农熵当作regularization的一个term，就能鼓励网络找到我们所期待的密度分布。

Smoothness Assumption

Smoothness Assumption认为对于接近的x，他们的标记y应该是相近的。换言之，近朱者赤近墨者黑；

下面是Smoothness Assumption的一个例子

通过“相似”的传递性，model可以给很多数据打上正确的标签。

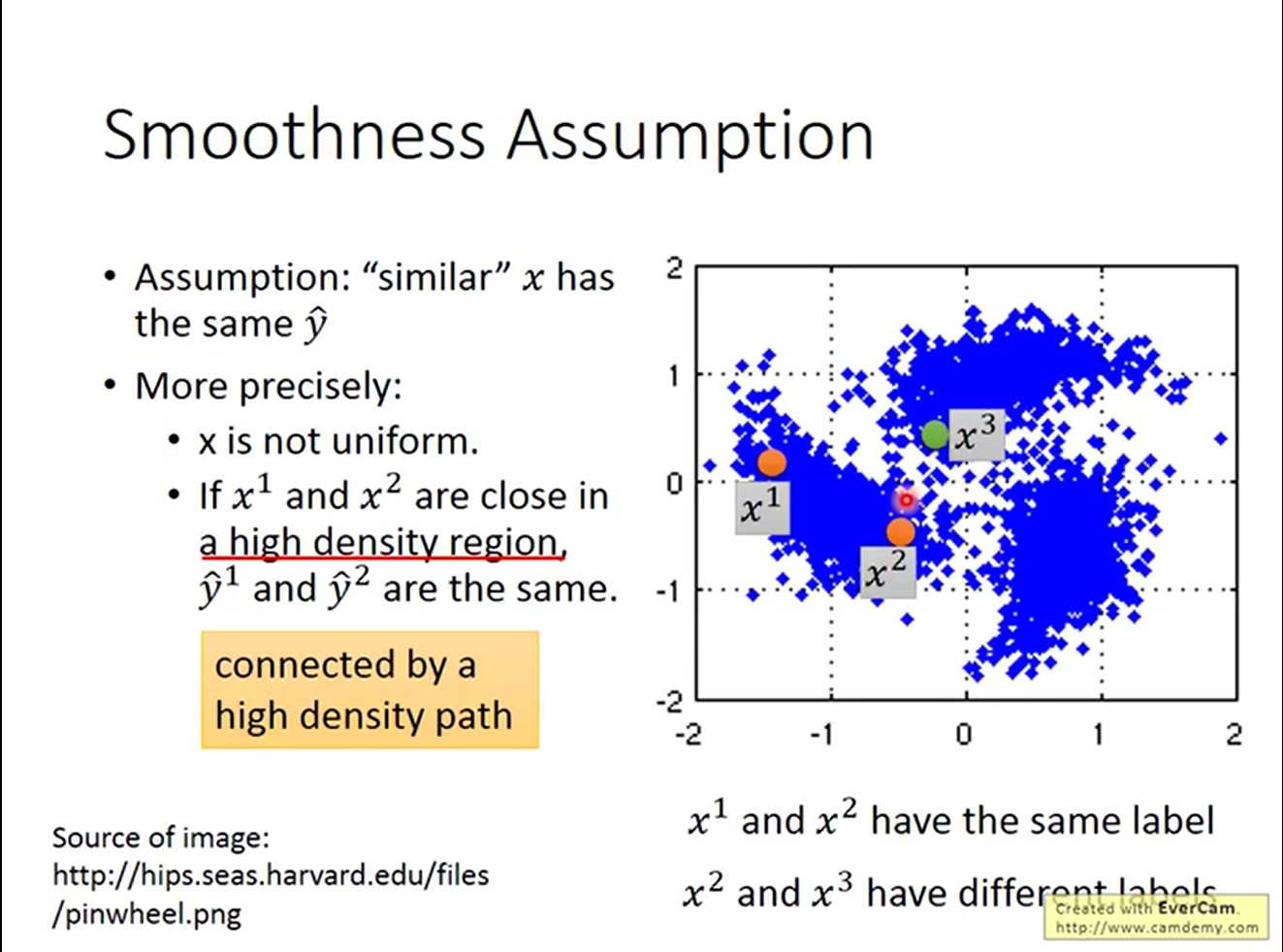比较正式的说法是，若x1和x2在一个高密度区域之内非常接近，那么y1和y2就是接近的；

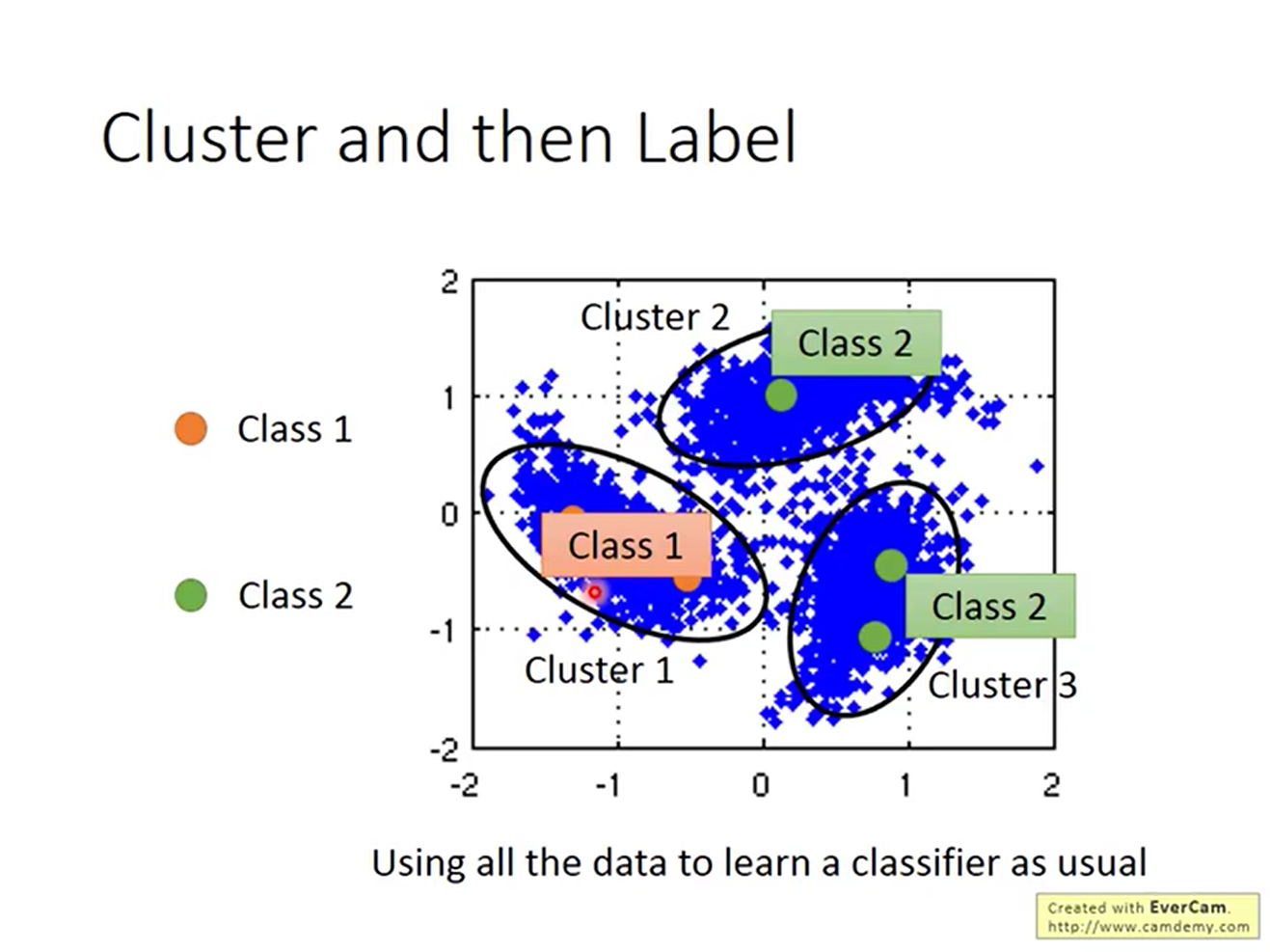
这和clustering比较类似。但clustering的数目并不好确定。因此引入了基于图的方法。

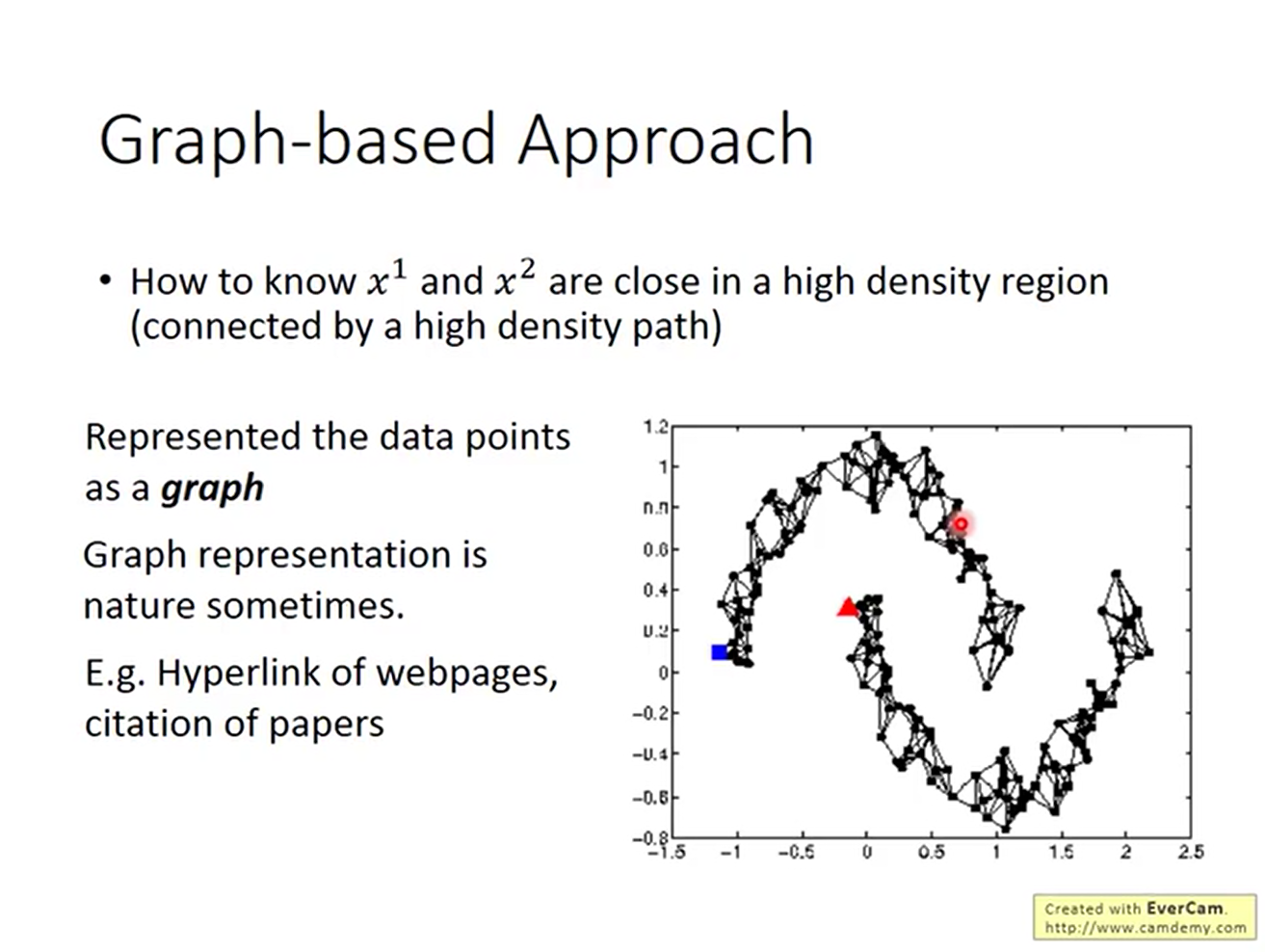将数据看作高维空间中的图，只需把图建立起来即可。

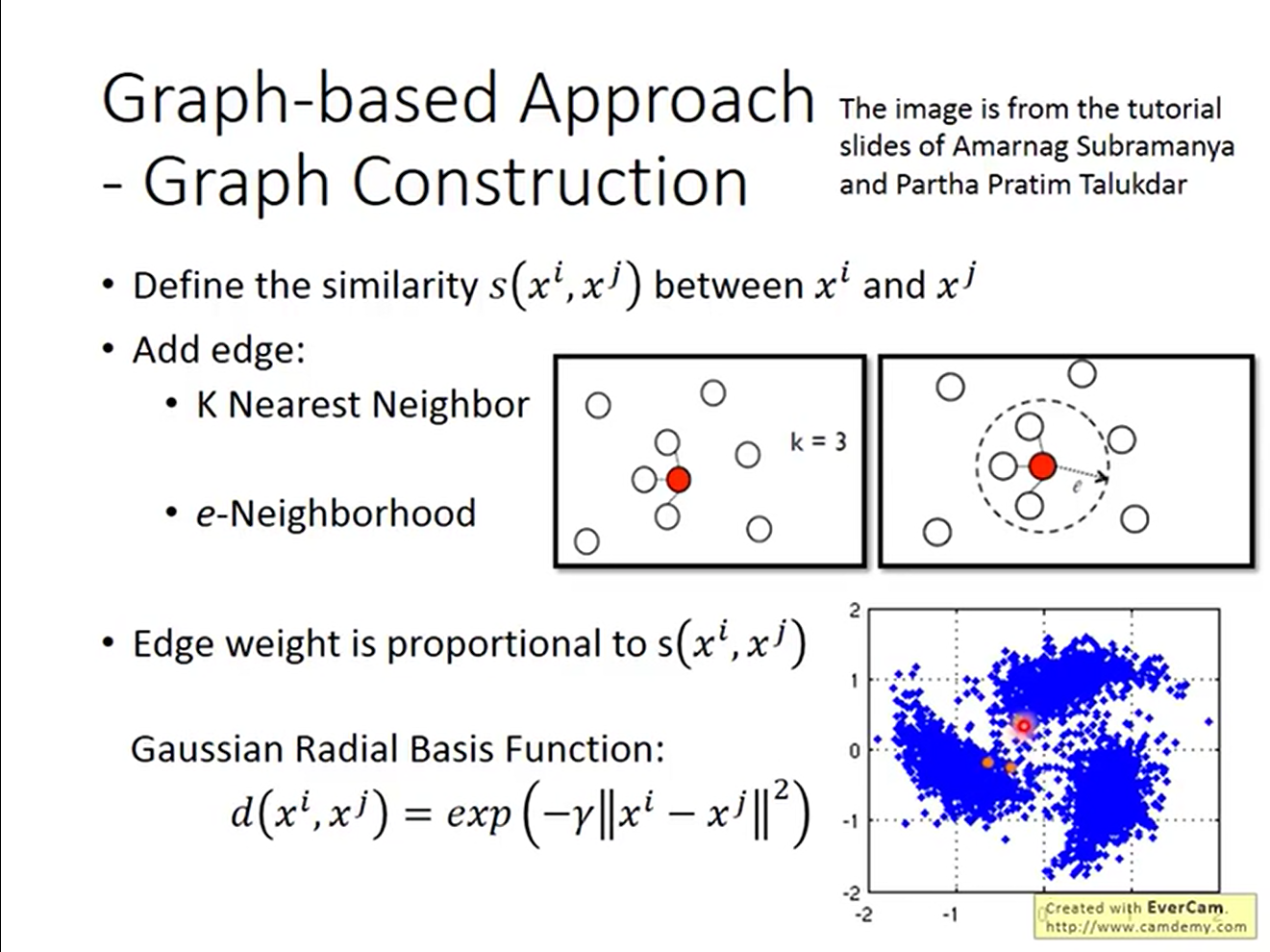
关于图的构建方法，有如下几种

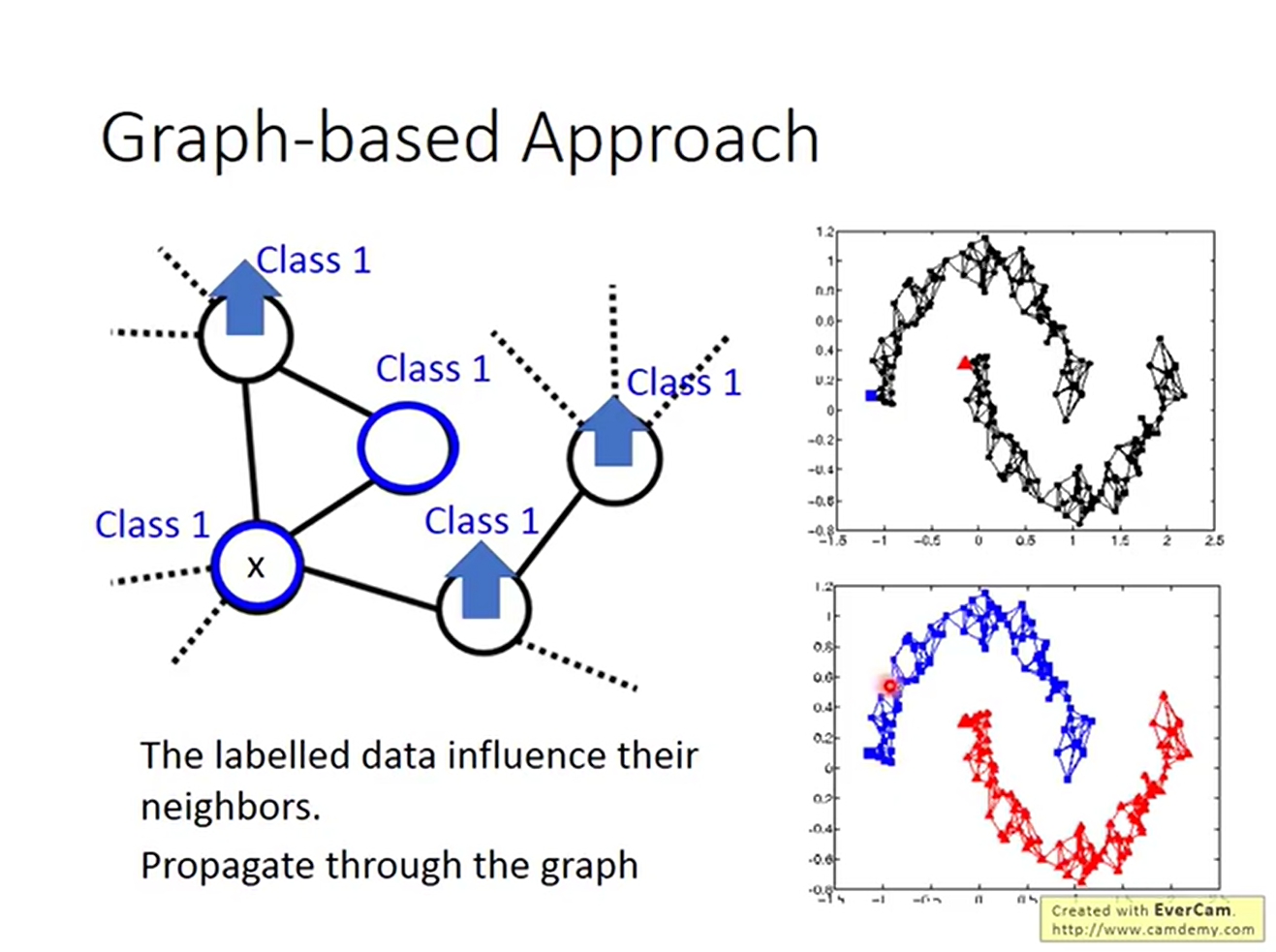
可以看到，通过构建图，一个点的影响可以扩散的很大一片区域：

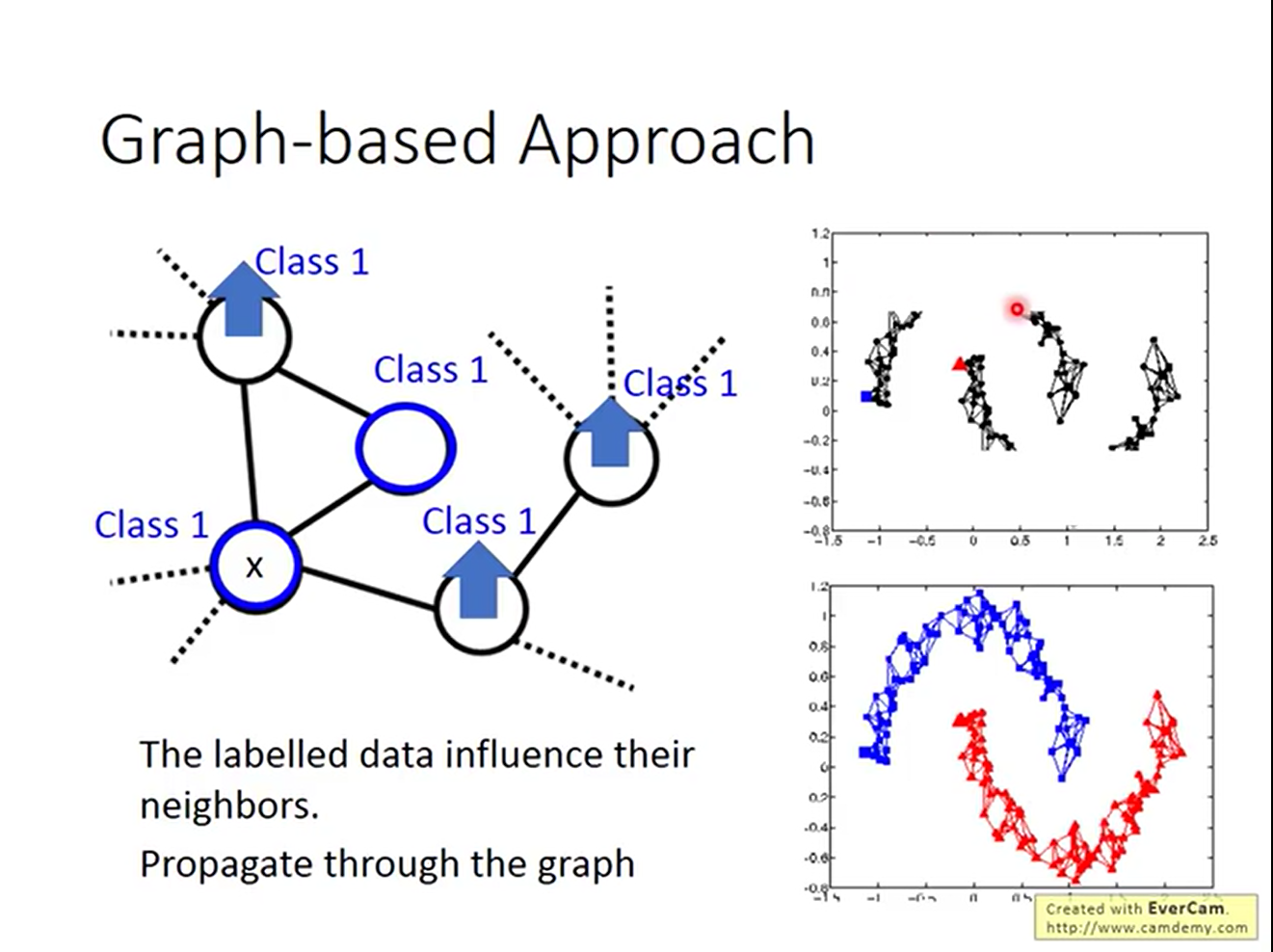
但图也有劣势。如果不能给每一个连通分量收集到一个数据点，这些unlabelled data就无法被计算相似度。

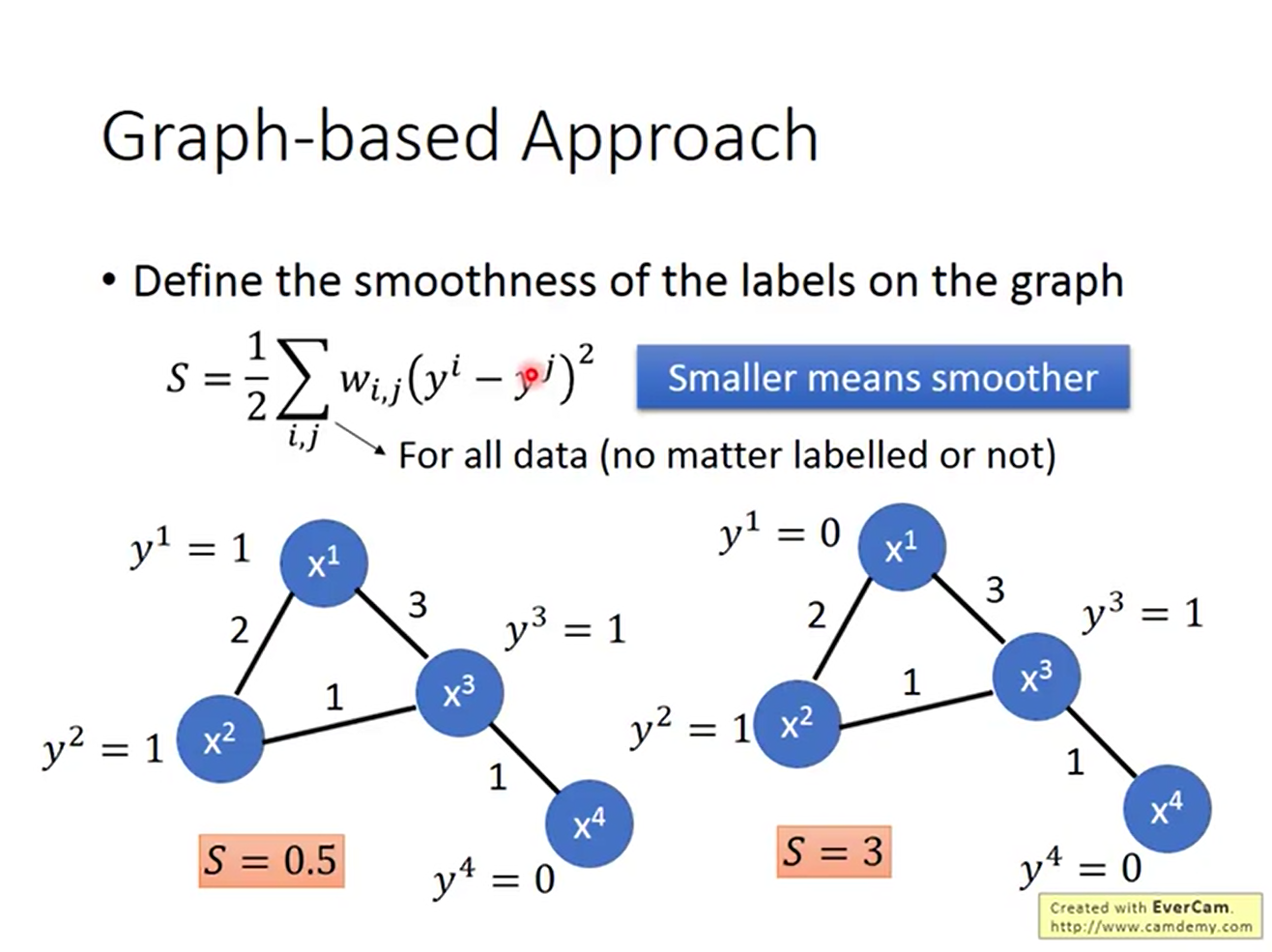
有了图之后就可以计算图的smoothness了。这时可以把smoothness当作网络的一个regularizer

Better Represerentation

对使用者来说，数据的呈现方式对使用的便利程度影响很大。例如罗马数字的除法就比阿拉伯数字的除法困难很多。

在机器学习中也是如此。使用更好的呈现方式会让学习事半功倍。关于如何找到更好的呈现方式，可以参考Autoencoders。