本文是NTU ML 2020中BackPropagation部分的笔记。

梯度下降是非常常用的优化算法。而在深度学习中，一个神经网络的参数动辄几百万，像线性模型那样人手工算好再告诉机器的方式已经不合适了，需要一种更高效的算法来计算梯度。

后向传播是计算梯度的高效算法，它的理论基础是链式法则。

$$p=\phi(x),q=\varphi(x),g=f(p,q) \\ \frac{dg}{dx}=\frac{\partial g}{\partial p}\frac{dp }{dx}+\frac{\partial g}{\partial q}\frac{dq}{dx}$$

---

梯度下降的目标函数total loss是各个example的和

$$L(\theta)=\sum_{n=1}^N C^{n}(\theta)$$

所以只需能计算出其中一项的loss就可求total loss的梯度。

考虑如下的一个3x2的神经网络

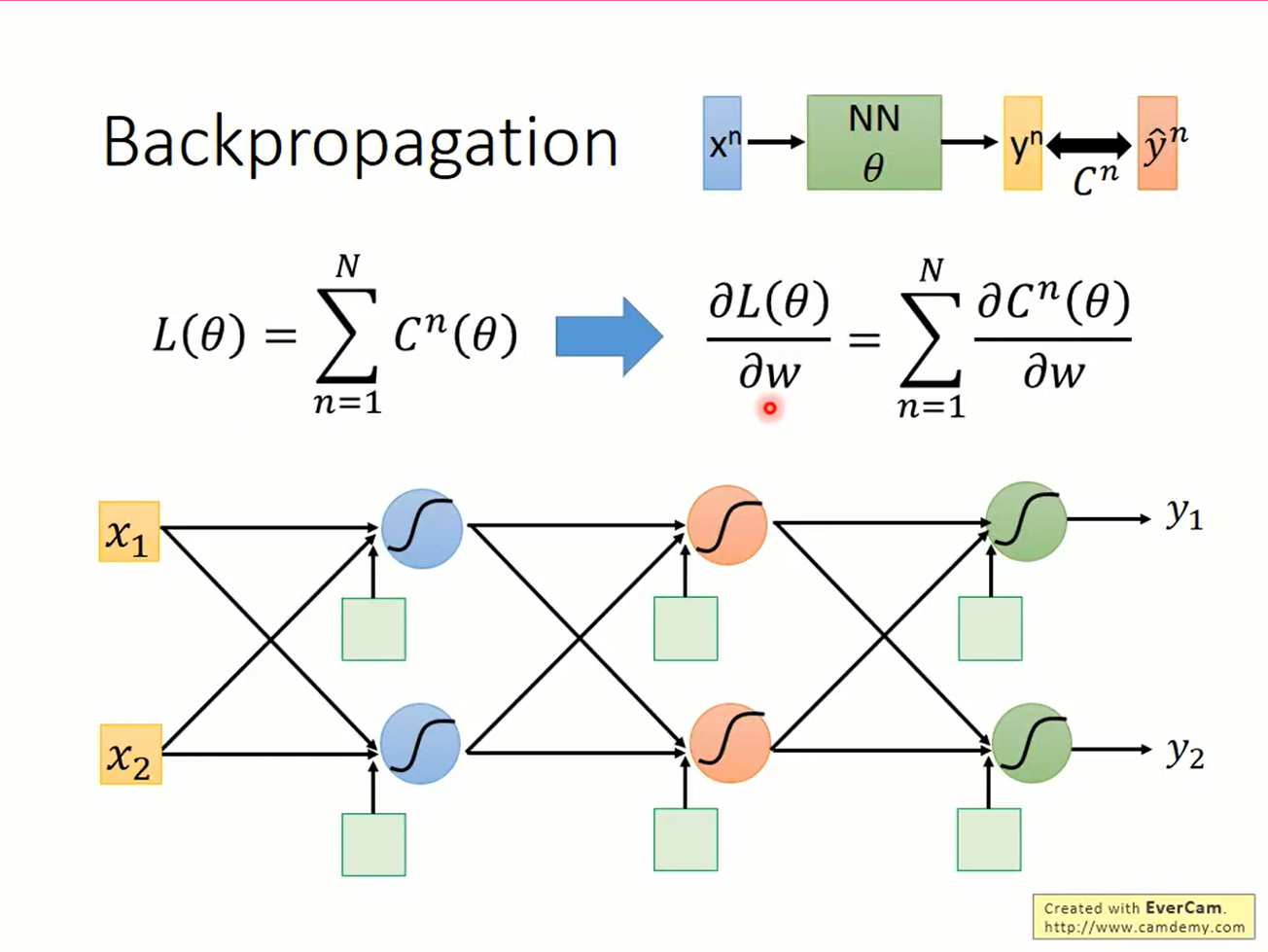
第一层第一个神经元的参数w1，输入激活函数的值z=w1*x1+w2*x2+b1
则由链式法则

$$\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial w_1}=\frac{\partial L}{\partial z}x_1$$

转化为求

$$\frac{\partial L}{\partial z}$$

考虑该神经元的下一层，z经过激活后的输出a被当作下一层的输入：

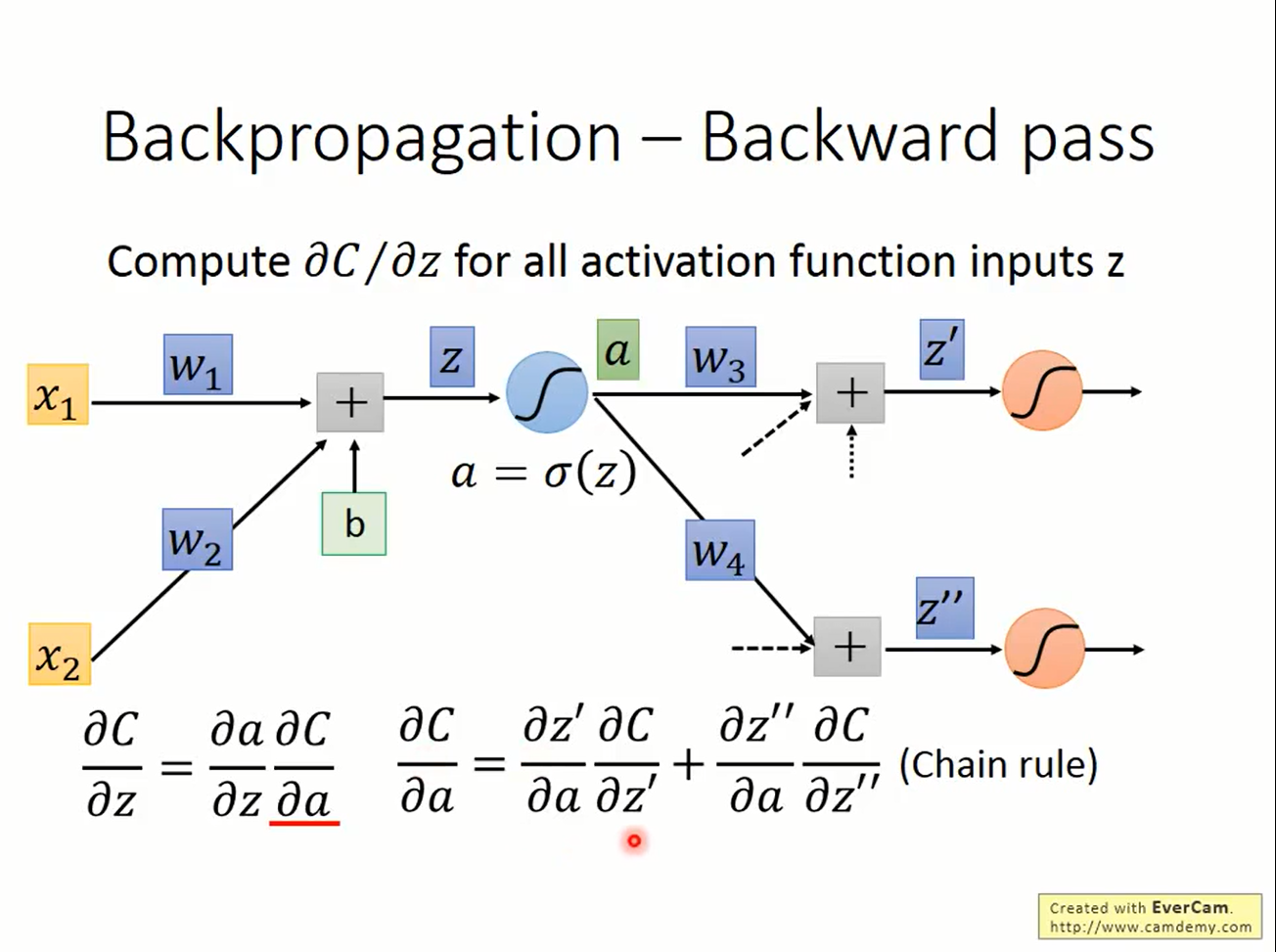则由链式法则，

$$\frac{\partial L}{\partial z} = \frac{\partial L}{\partial a}\frac{\partial a}{\partial z}=\frac{\partial L}{\partial a}\sigma'(z)$$

观察到a已经变成了下一层网络的输入，问题又化为了最初求loss对网络输入的微分，但问题的规模-求梯度的“层数”却减少了一层。思维敏锐的同学可能已经发现了，这是分治法。

让我们更进一步

$$\frac{\partial L}{\partial a}=\frac{\partial L}{\partial z'}\frac{\partial z'}{\partial a}+\frac{\partial L}{\partial z''}\frac{\partial z''}{\partial a} = \frac{\partial L}{\partial z'} w_3+ \frac{\partial L}{\partial z''} w_4$$

从而

$$\frac{\partial L}{\partial z}=\sigma'(z) \left[\frac{\partial L}{\partial z'} w_3+ \frac{\partial L}{\partial z''} w_4 \right]$$

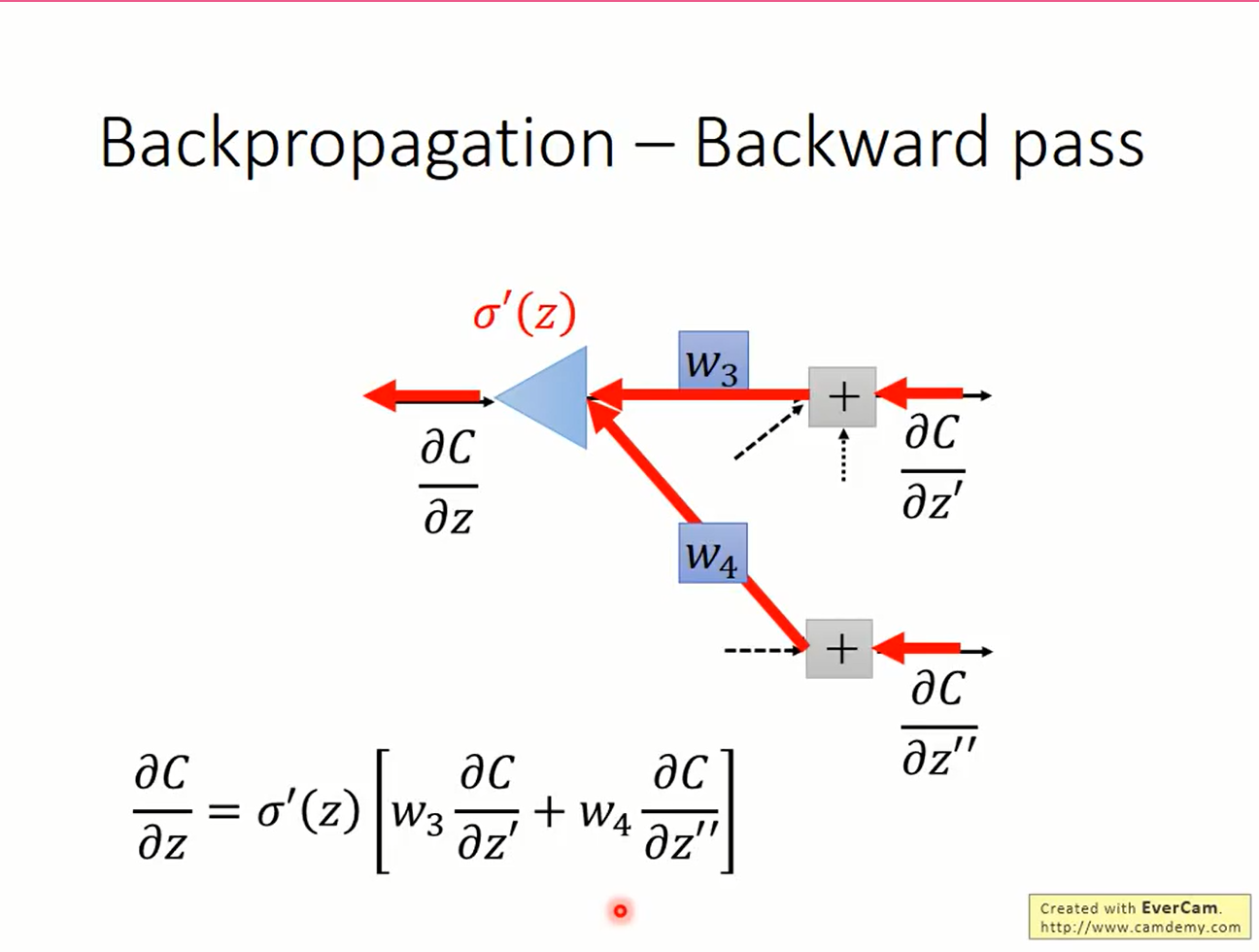
看起来就像是一个以偏微分为输入,y=σ'(z)x为激活函数的神经元的输出

考虑所有激活函数的输入z，当前层的偏微分z与后一层之间的偏微分z'存在计算上的依赖关系。因此计算loss对z的偏微分时，要从后往前算。因此得名backward pass。

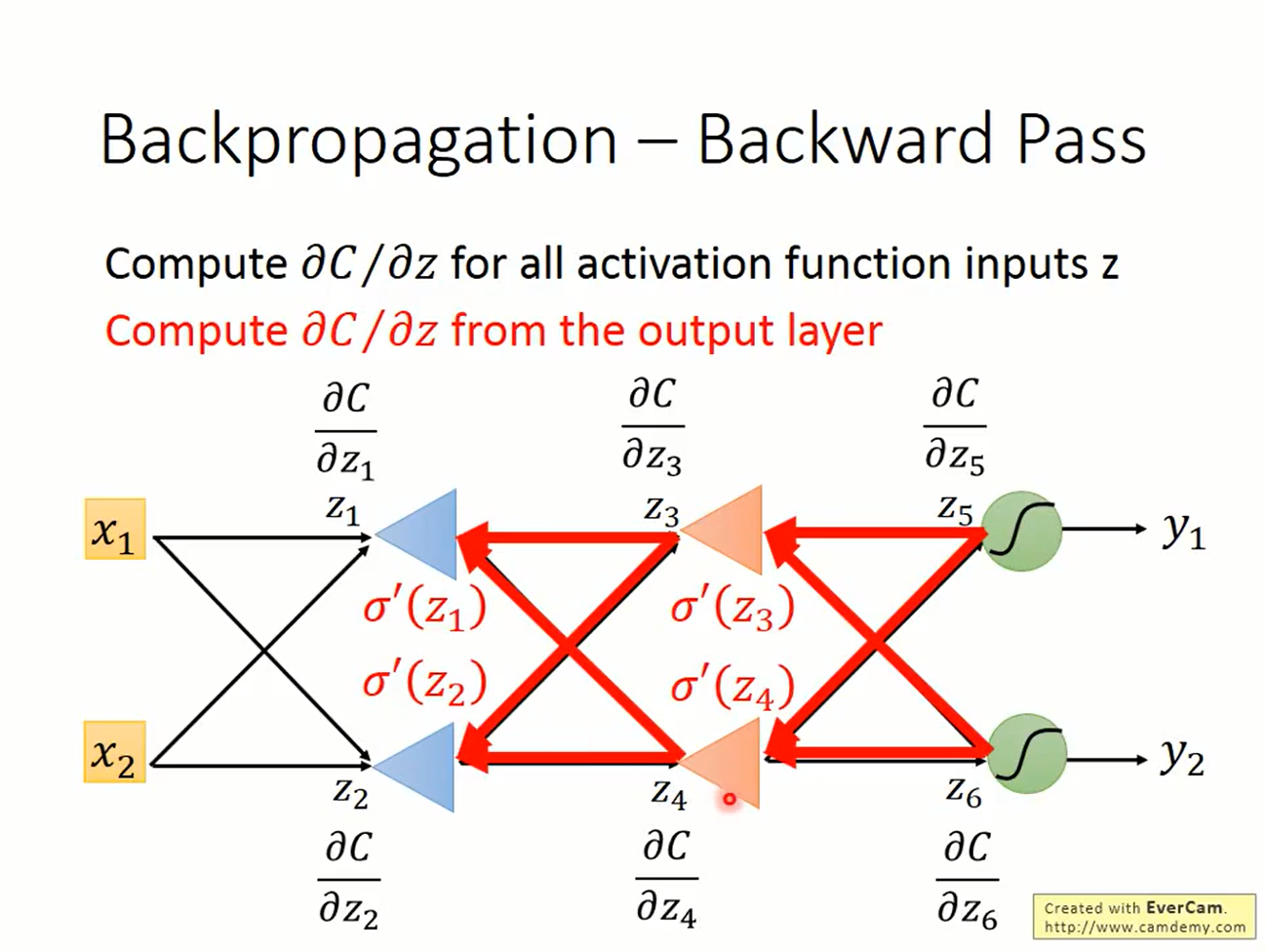
而计算本层神经元的输入a时是从前往后算的，因此叫做foreward pass

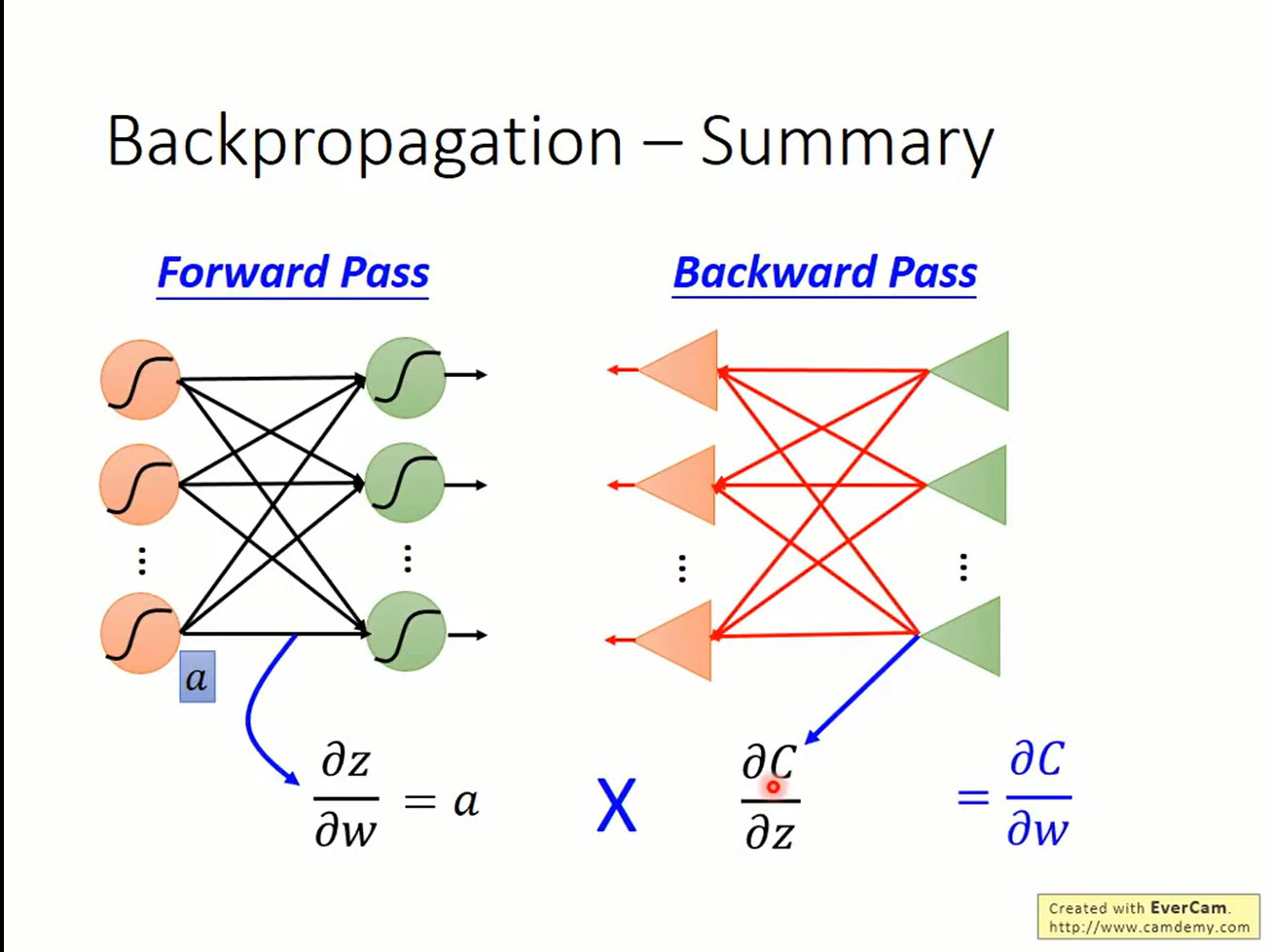
总结一下，要计算L对参数w的偏微分需要进行两个步骤：

1. foreward pass. 算出L对当前层神经元的输入a的偏微分。从前往后算。
2. backward pass. 计算出L对当前层激活函数的输入z的偏微分。从后往前算。

两者相乘，即得

$$\frac{\partial L}{\partial w}$$