任何一个机器学习的任务都可以被拆解为三步

1. 找到一组函数(model)
2. 找到评价函数好坏的标准(loss)
3. 找出最好的函数(optimization)

这三步在神经网络中同样成立。但在神经网络中，要找的不是一组函数，而是一种网络架构(architecture)。本文中的卷积神经网络(CNN)就是一种网络架构

根据universal approximation theorem，MLP已经足够表达任意函数。而在实际中，因为相邻层级的神经元之间的任意互联导致MLP容易过拟合。而在处理一些具有结构化的输入时，MLP中又会有大量的参数重复。为了解决这些问题，引入了CNN。

Why CNN?

考虑这样一个问题：如何让机器认出图片里的一张鸟？

回顾人类的思考过程，若图片中的物体具有鸟的基本特征，如喙、翅膀和爪，则认为它是鸟。在这个过程中，我们并不关心翅膀在图片中的位置：只要有喙就可以了。对翅膀和爪也是同样成立。

继续思考，怎么认出喙？喙可以由它的边界(geometry)来定义：两条斜线围成的尖尖的多西。翅膀和爪也可以有对应的边界来定义。同样的，我们并不关心边界出现的位置，只要它能确定这个物体是个喙就可以了。

实际上这就是CNN出现的动机之一：我们只关心一些模式是否出现，而不关心它们出现的位置。换句话说，我们所期待的模式会在图片的不同区域出现。

回到图像的例子上，人们发现了三个属性：

1. 比起整张图片，模式通常是比较小的
2. 相同的模式会在不同的区域出现
3. 对图片做subsampling(如删掉奇数行和偶数列)并不会改变图中的物体

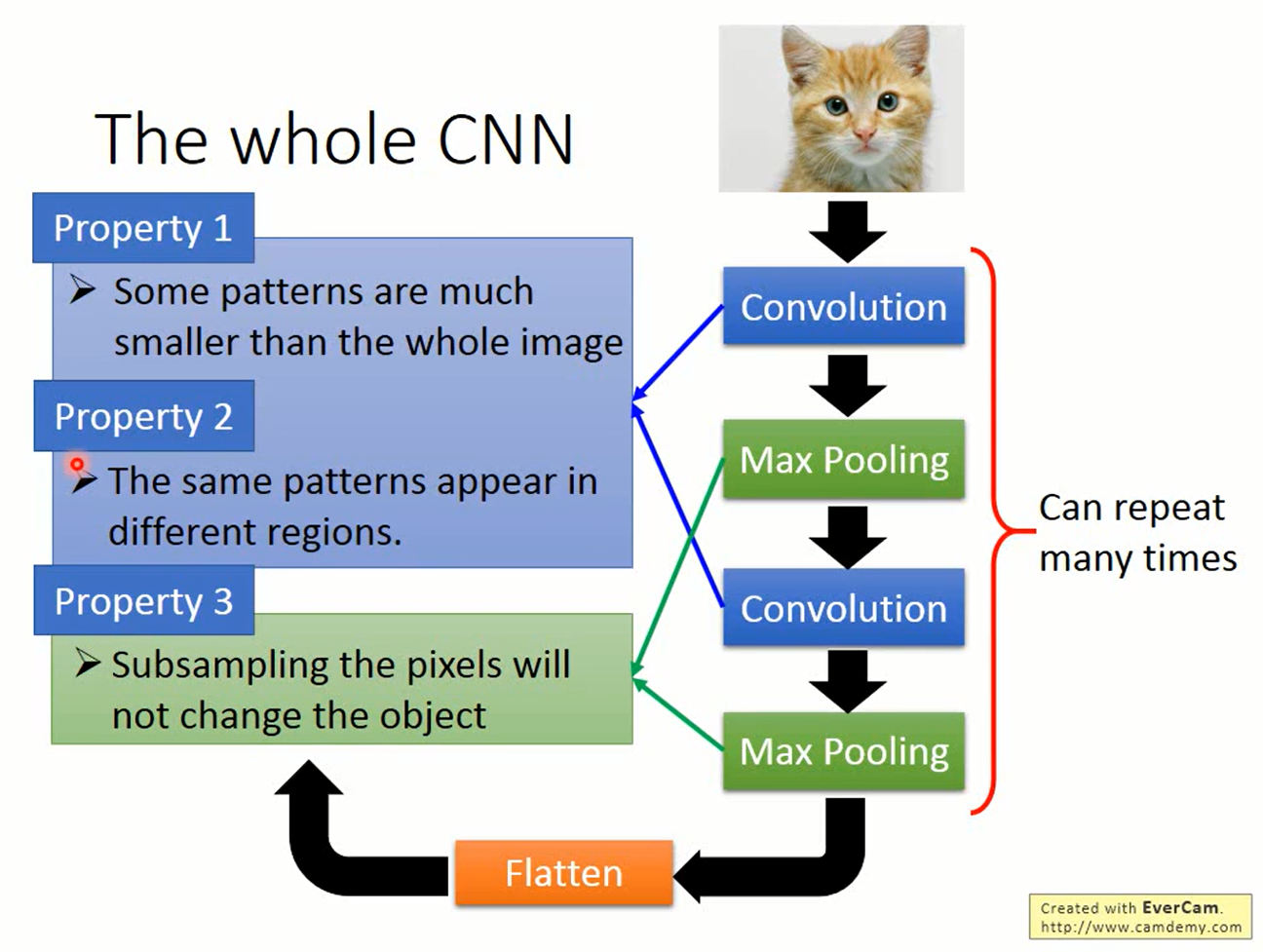
基于这三种属性，人们提出了convolution和pooling两种操作。convolution对应属性1、2，pooling对应属性3。convolution和pooling交替就是CNN的架构。

Convolution

Convolution的基础单位是filter(kernel)。filter是一个矩阵，用来检测模式
考虑如下的情景

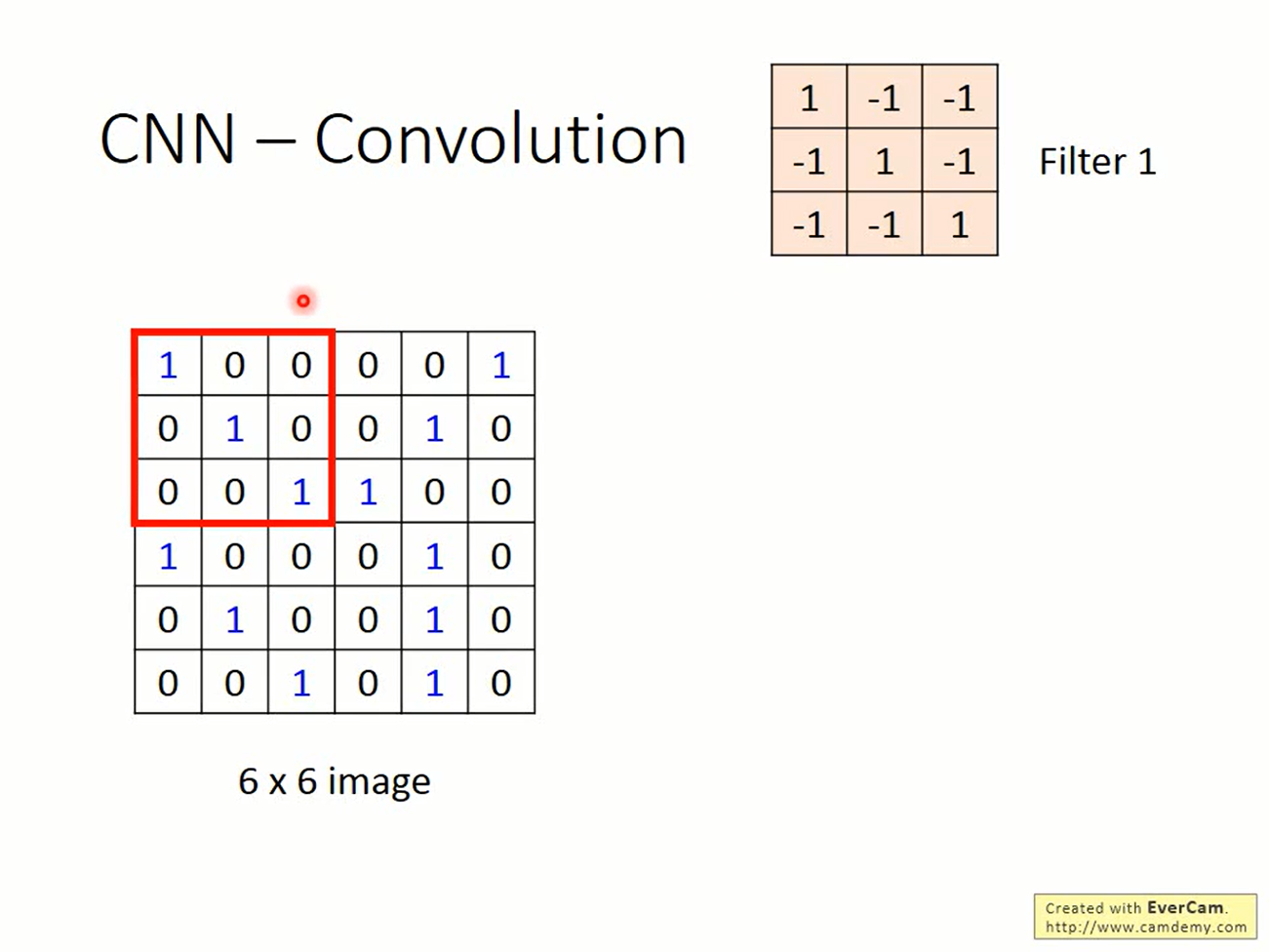
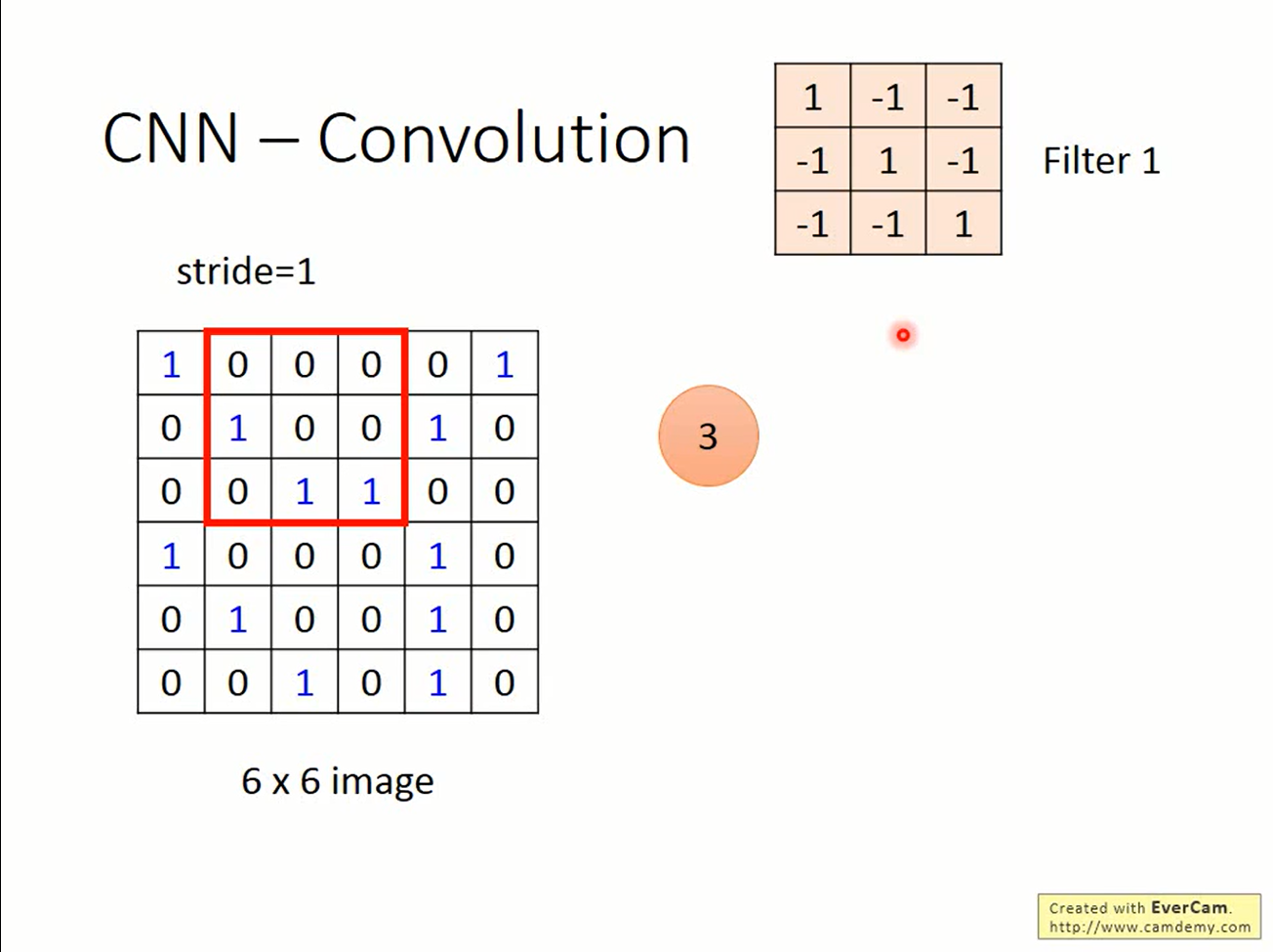
输入是6*6的图片，filter是3*3的矩阵。在图片的左上角找到一个与filter一样大的矩阵，做element-wise product，会得到一个数值。将filter往右移动一格，继续这个步骤，就又得到新的数值。移动的距离称为stride(步长)

filter通常比输入更小，而filter在移动的过程中可以在不同的位置上检测出对应的模式。这就体现了属性1和2。

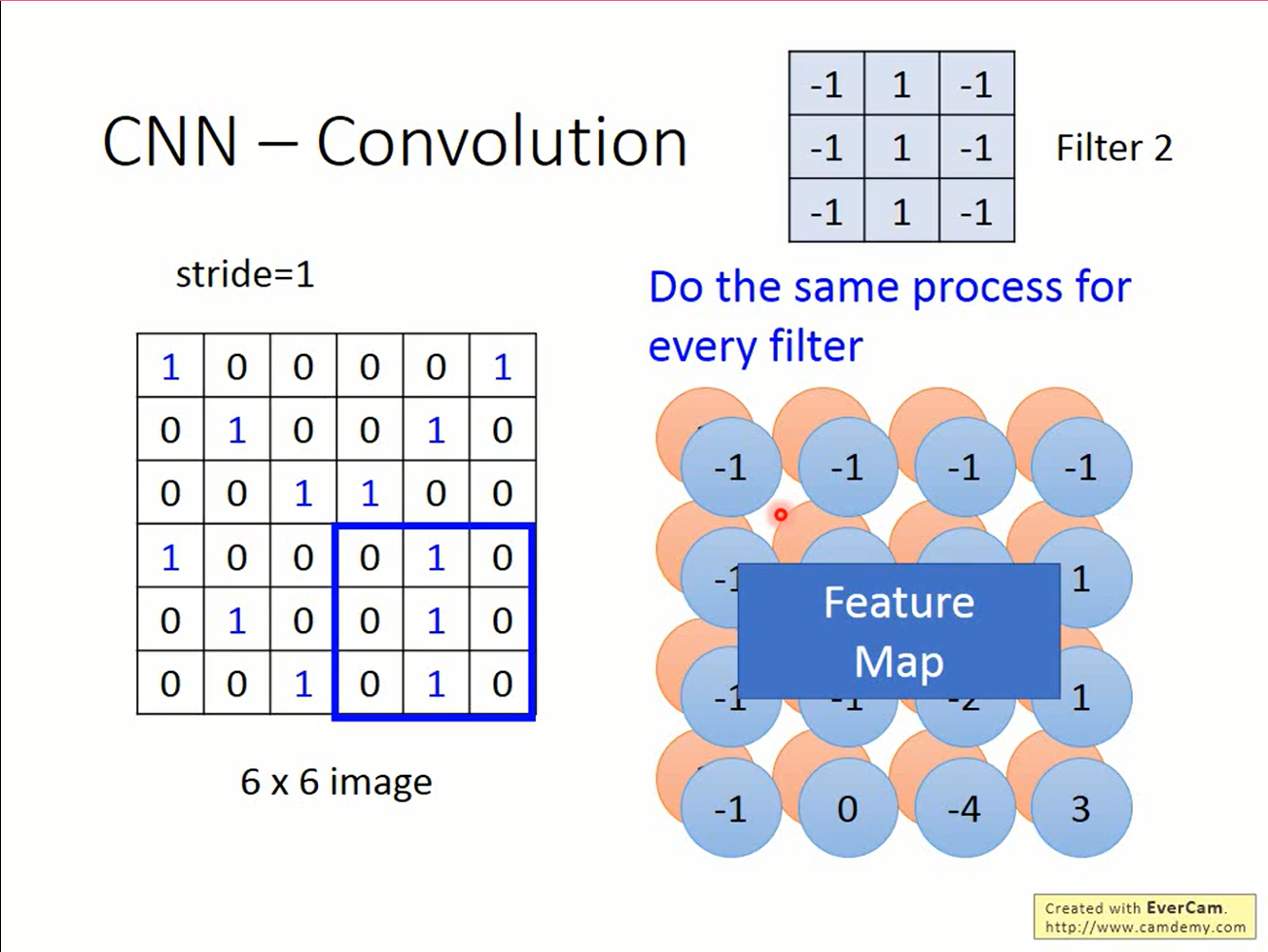
filter移动完毕后会得到一个新的矩阵。我们可以使用多个filter,将这些filter的输出放在一起会得到一个三维的张量，称为feature map.

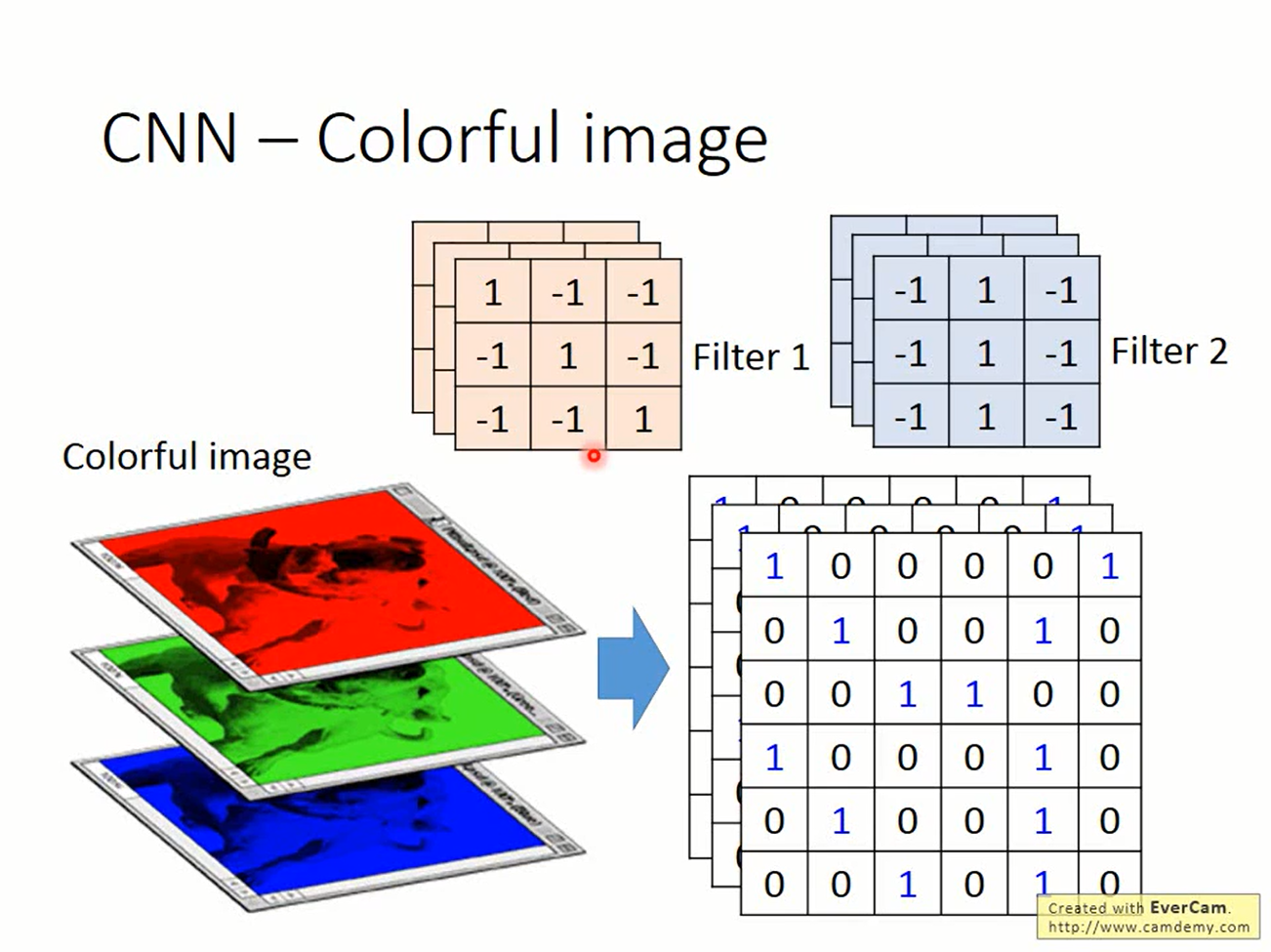输入也不一定是黑白的。若输入彩色图片，则需要一个三维的张量来表示

$$\mathrm{V}_{c,i,j}$$

这时的filter也是一个三维张量。
这里的重点是，不管输入是什么样，filter的“z轴”要与输入的“z轴”一样高，然后在其他轴上以stride移动，得到的标量集合起来成为新的张量作为下一层的输入。
Convolution得到的feature map会缩小，这可以补零(zero padding)来避免

实际中通过在MLP中共享参数来实现。使用了更少的参数来做同样的事情就不容易过拟合。

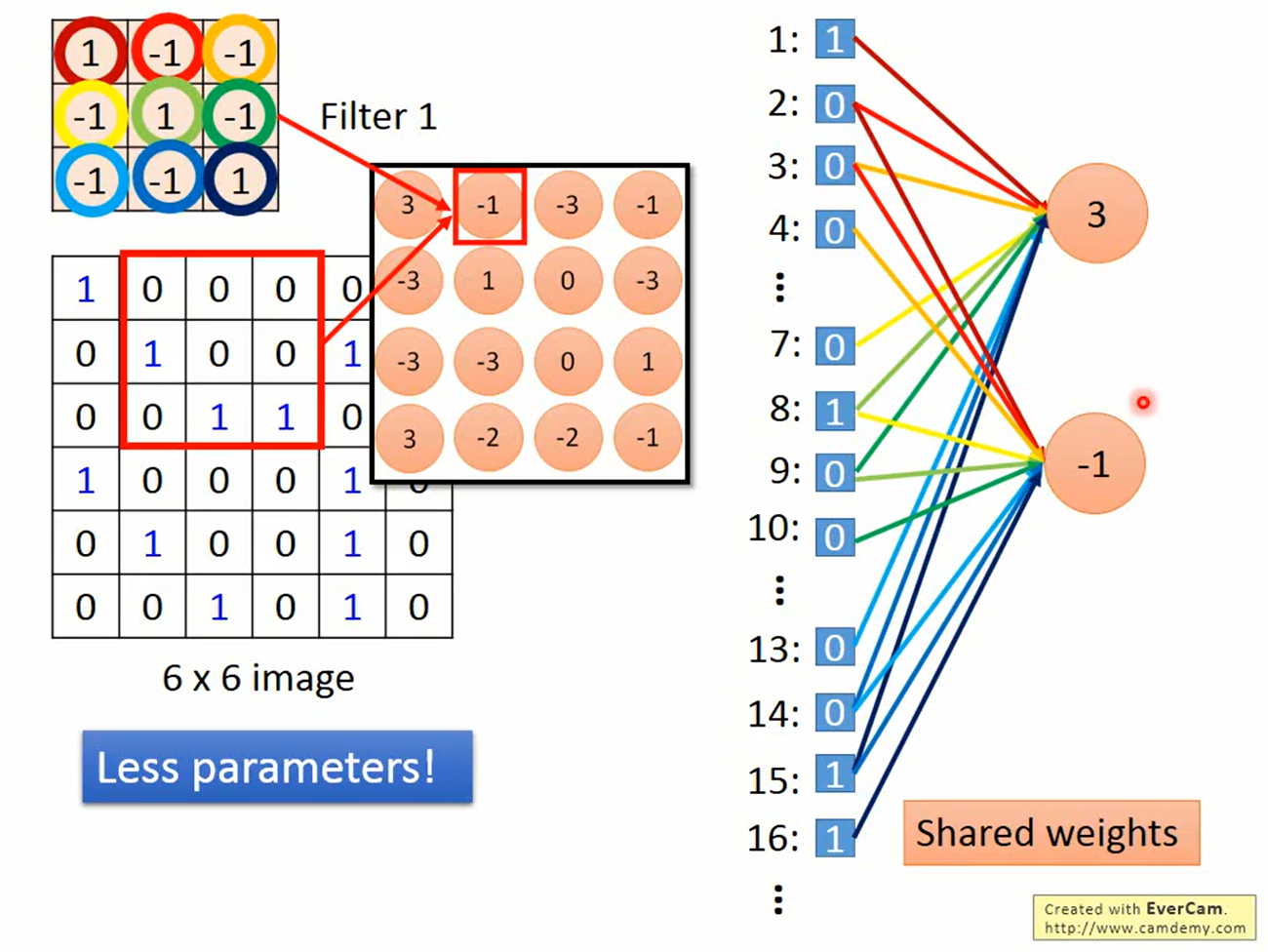
Pooling

Pooling的思路更简单了。对一些区域进行采样，得到一张更小的image,这就是属性3。

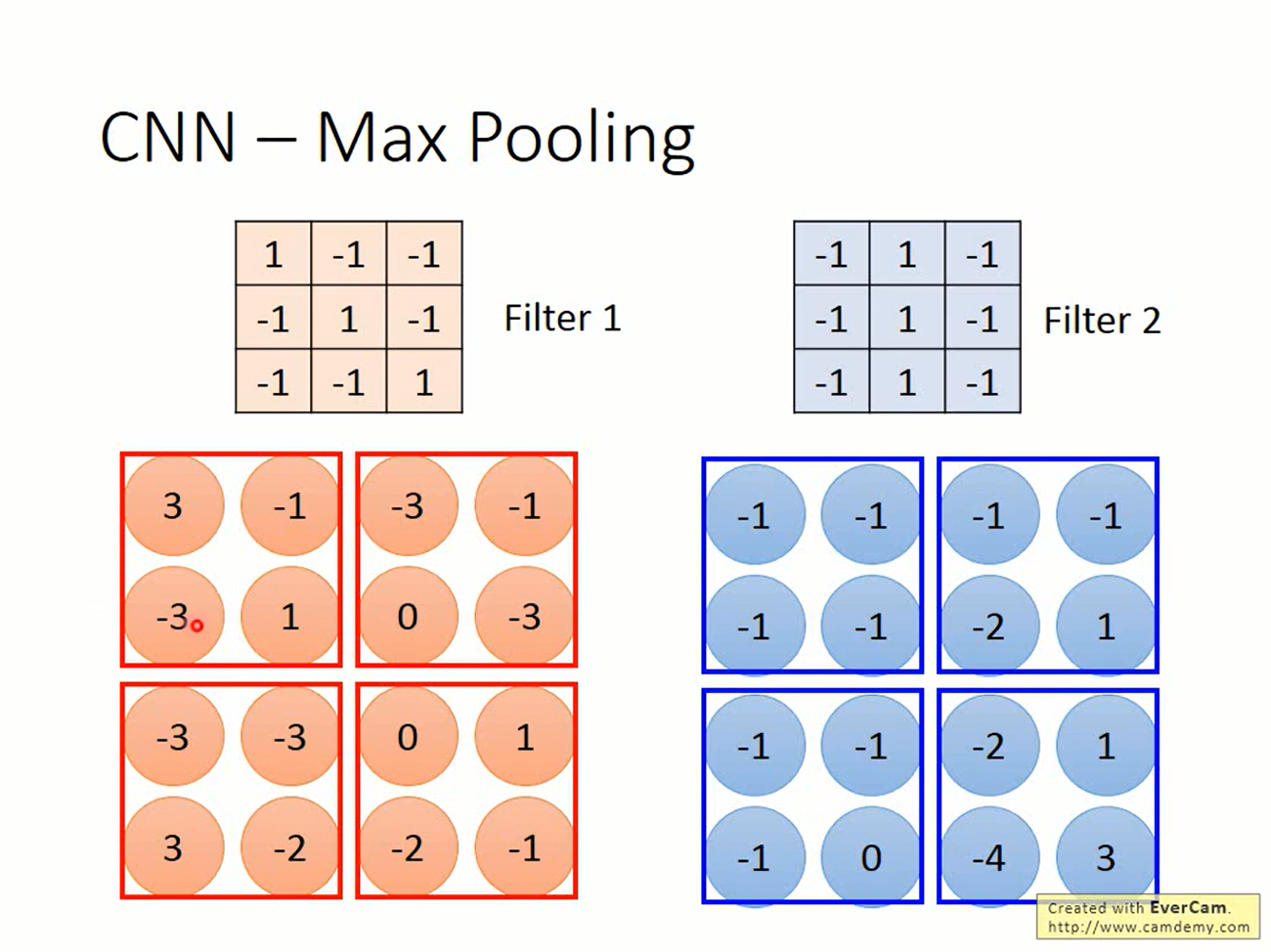
pooling有很多选择，可以取算术平均，可以取L2 norm。一般比较常见的是max pooling。

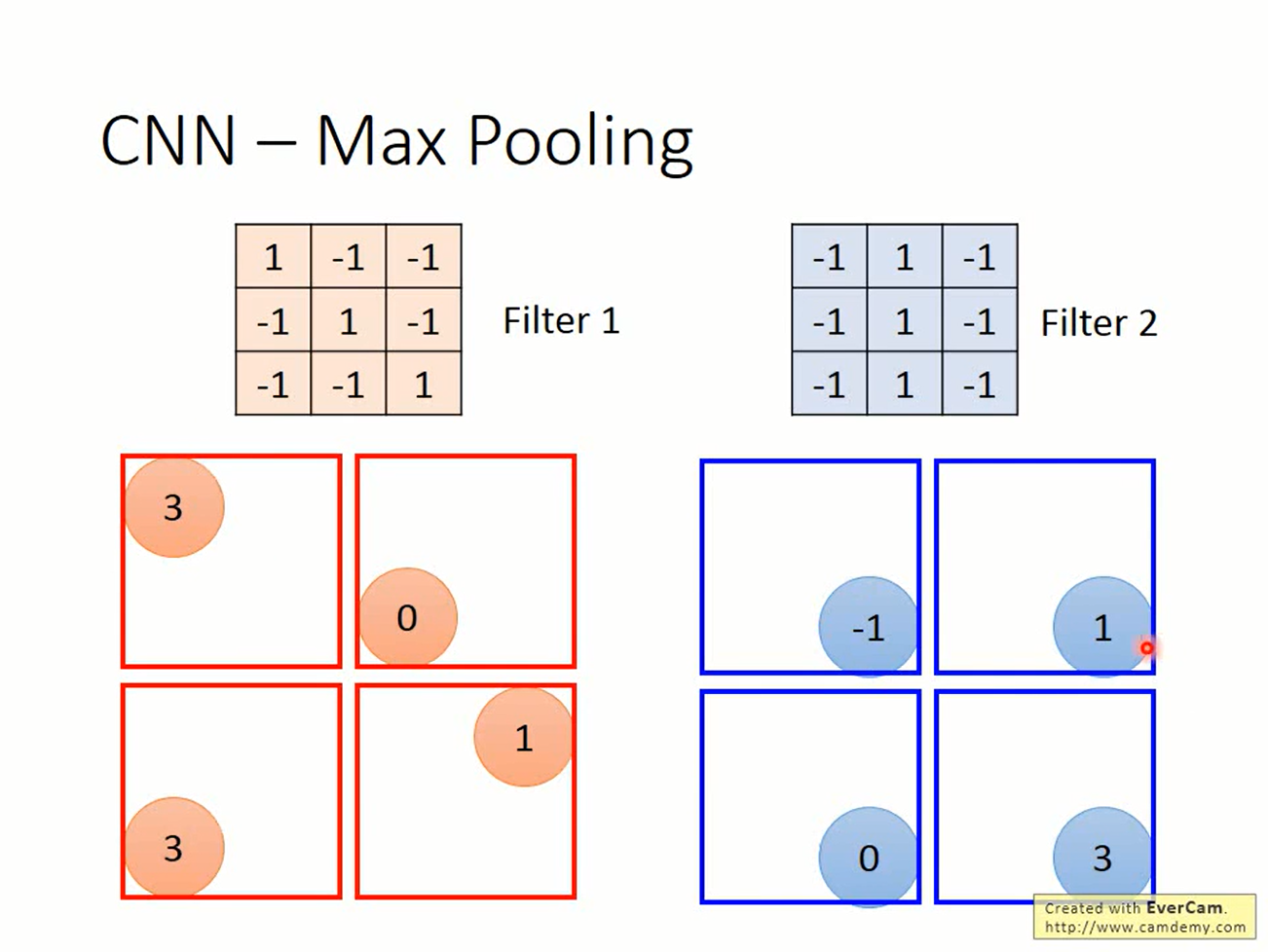
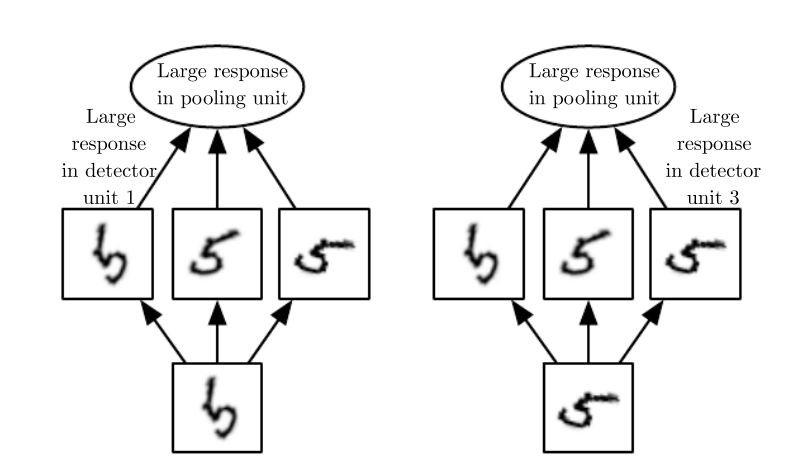
通过pooling，网络就可以对输入中比较规律的变化不那么敏感。这称为invariance。

Flatten

做完pooling后得到的是一个张量。把它“拉直”成一个向量，丢给MLP就可以实现我们所要做的事情了。

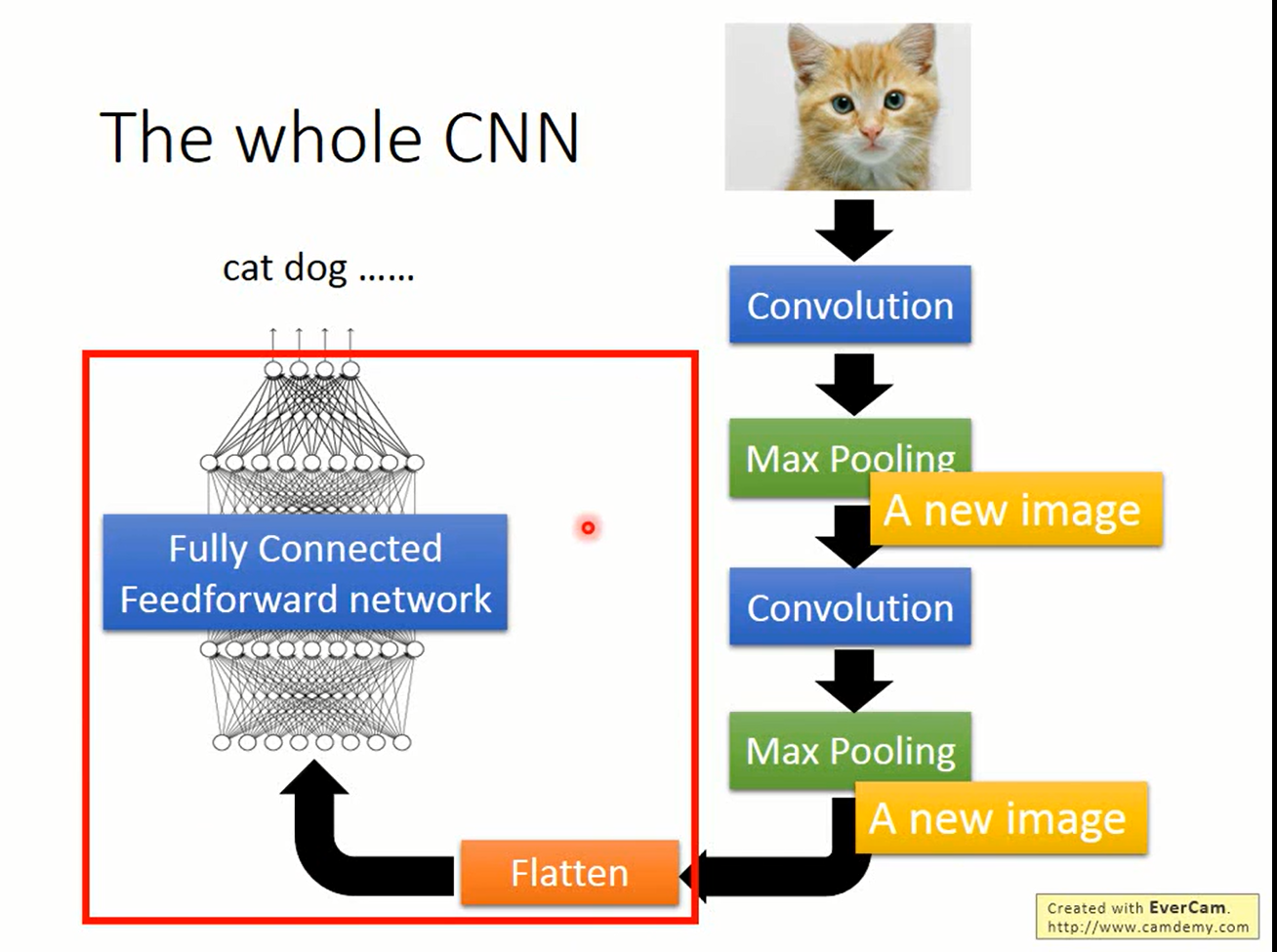
CNN并不只能用于图像处理，只要要处理的问题具有上述的三个属性，就可以用CNN来解决。
下面是一些用CNN效果比较好的任务: